Rotation Matrices
The matrices in the following animations are at the heart of computer graphics. They describe objects moving in three-dimensional space and are essential to MATLAB's Handle Graphics, to Computer Added Design packages, to Computer Graphics Imagery in films, and to most popular video games. Many modern computers contain GPUs, Graphic Processing Units, which are optimized to compute the product of these matrices.
Contents
Rotations
The homogeneous coordinates system used in today's computer graphics software and hardware makes it possible to describe rotations, translations and many other operations with 3-by-3 and 4-by-4 matrices. These matrices operate on vectors with the position of an object, x, y and z , in the first three components.
Rotations about the coordinate axes are described by three matrices. Rotations about the x -axis are produced by $R_x$, which rotates y and z, while leaving x unchanged.
$$ R_x(\theta) = \left( \begin{array}{rrr} 1 & 0 & 0 \\ 0 & \cos{\theta} & -\sin{\theta} \\ 0 & \sin{\theta} & \cos{\theta} \end{array} \right) $$
Rotations about the y -axis are generated by
$$ R_y(\theta) = \left( \begin{array}{rrr} \cos{\theta} & 0 & -\sin{\theta} \\ 0 & 1 & 0 \\ \sin{\theta} & 0 & \cos{\theta} \end{array} \right) $$
And, rotations about z are provided by
$$ R_z(\theta) = \left( \begin{array}{rrr} \cos{\theta} & -\sin{\theta} & 0 \\ \sin{\theta} & \cos{\theta} & 0 \\ 0 & 0 & 1 \\ \end{array} \right) $$
theta
Rotation angles are specified in degrees. Our MATLAB programs use the degree-based trig functions cosd and sind. Here are graphs of $\cos\theta$ and $-\sin\theta$ , evaluated with the angle $\theta$ going from 0 to 360 degrees in 10-degree steps.

Compass
Here is another look at the same data, cosd(theta) and -sind(theta) for theta = 0:10:360. The columns of the rotation matrix are the coordinates of the rotating dots. The blue dot starts at (0,1) and the orange dot starts at (1,0).
If you drop the zeros from the values of theta, you are left with the integers from 1 to 36. This is the numbering in the international standard describing the compass direction of runways at airports. The initial position of our blue dot corresponds to runway 36 and the orange dot starts as runway 9.

Roll, Pitch, Yaw
Note: Refresh your browser to synchronize these animations.
For aircraft and space vehicles, rotation around the x-axis from nose to tail is known as roll.
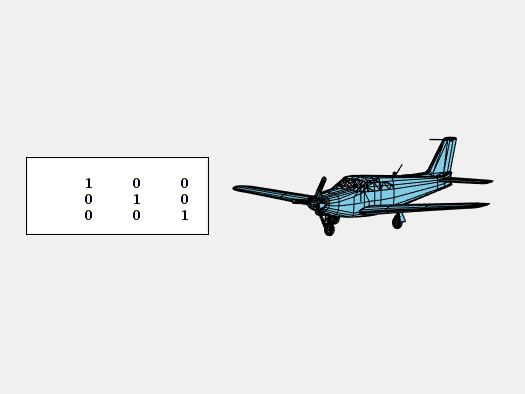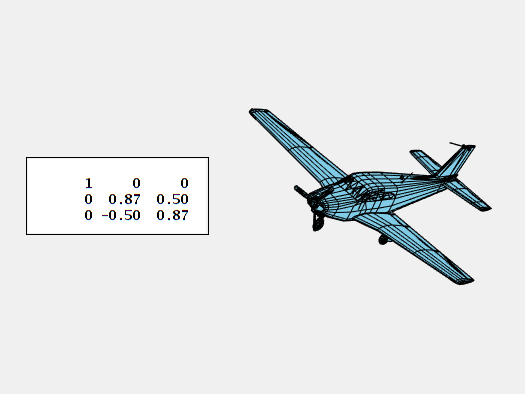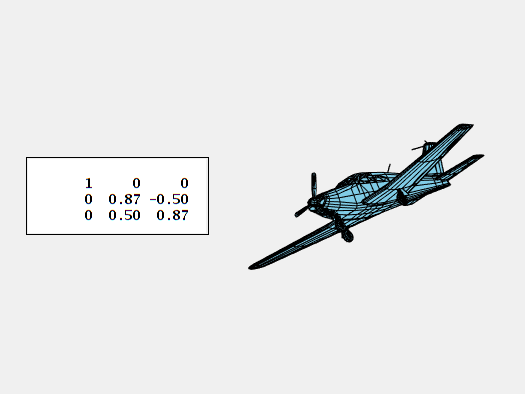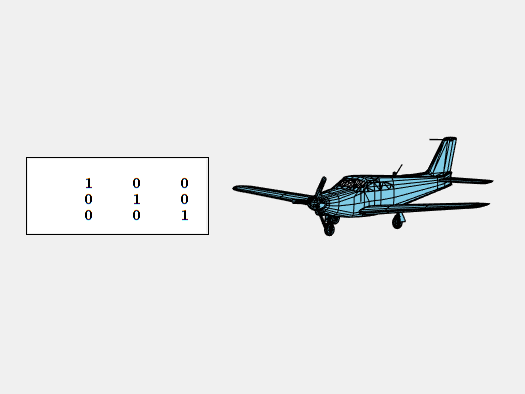
Rotation about the y-axis parallel to the wings is pitch.

And, rotation about the vertical z-axis is yaw.

Propeller
Our model of the Piper PA-24 Comanche has 97 patches. One of them is the propeller. This animation of a rotating propeller is very similar to our earlier animation of the compass.

Cubelet
Qube, our digital Rubik's Cube simulator, uses 27 copies of a single cubelet. This animation of a rotating cubelet shows a quarter turn clockwise about x, followed by a quarter turn clockwise about y and then a quarter turn counterclockwise about z. If these three rotations are repeated four times, the cubelet returns to its initial orientation. In the process, we see the traditional Rubik's colors of all six faces -- white, green and orange opposite yellow, blue and red.

Scramble
Note: Refresh your browser to synchronize these animations.
Rubick's Cube is all about rotations. Rotating the cubelets in any face of the puzzle, while leaving the rest of the puzzle fixed, is called a "move". Like any cube, Rubik's cube has six faces. Each move rotates one of the six faces in either a clockwise or counterclockwise direction. So, after n moves, the puzzle is in one of 12^n possible states. The challenge is to return the cube to its original orientation.
Here are six random rotations produced by scramble(6). Because 12^6 is 2,985,984, this is just one of almost three million six-move scrambles.

Unscramble
One possible way to restore any starting condition is to retrace the moves that produced it. This is the "follow the breadcrumbs" algorithm. So, I call this unscramble, rather than solve.

Exercises
- 1: Which rotation matrices and what values of theta are used in the animations?
- 2 (not easy): When is unscamble a solution with the minimum number of moves?
Software
The source code for Qube is available from this link: Qube_May18_osf.m. The osf, one single file, format is a self-extracting archive that expands into a directory of individual functions.









댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.