Experience With Chatbots Generating MATLAB
A friend is investigating the use of generative AI in his classes. I asked two different popular chatbots to write MATLAB programs for a mathematically nontrivial problem. Both chatbots understood my query and both wrote plausible MATLAB programs, but one of the programs was not correct. My recommendation for coursework: carefully read and test programs produced by generative AI and repair any incorrect ones.
Contents
Redheffer, Mertens and Ahalt
Frequent readers of this blog know about my recent obsession with Redheffer matrices and the Mertens conjecture. So, when my friend Stan Ahalt visited from North Carolina State a few days ago, and wanted to discuss the use of generative AI in the new Data Science curriculum, I suggested asking chatbots to write MATLAB programs that check the Mertens conjecture.
We logged onto the web sites for two different AI companies. Our query was the same at both sites.
Please write a MATLAB program to test the Mertens conjecture.
I was pleasantly surprised when both systems knew about MATLAB and understood the query. One of the systems replied:
Certainly! I'll create a MATLAB program to test the Mertens conjecture. First, let me briefly explain what the Mertens conjecture is, and then I'll provide the code. The Mertens conjecture states that the Mertens function M(n) is bounded by √n for all positive integers n. Mathematically, it can be expressed as:
|M(n)| ≤ √n for all n > 1
Where M(n) is the Mertens function, defined as the sum of the Möbius function μ(k) for all positive integers k up to n:
M(n) = Σ μ(k) for k = 1 to n
Here's a MATLAB program to test this conjecture.
Program number one
The program from one of the web sites begins:
function M = test_Mertens(n) % Function to test the Mertens conjecture for a given n % Returns true if the conjecture holds for all values up to n, false otherwise
This is followed by code to sum the Möbius function and verify that abs(M) < sqrt(n). The crucial mobius is a straight-forward implementation of the definition. The code relies on MATLAB intrinsics, factor and unique.
function mu = mobius(k)
% Function to calculate the Möbius function of k
% Factorize k
p = factor(k);
% Check for square factors
if length(p) ~= length(unique(p))
mu = 0;
else
mu = (-1)^length(p);
end
end
I was very pleased. The entire program is only 40 lines long, eminently readable, and correct.
Program number two
The program from the other web site is more sophisticated. It knows enough about MATLAB to use its cumulative summation.
M = cumsum(mu);
Here is the crucial mobius function. At first glance, it looks OK. Is it?
function mu = mobius(n)
% Calculate Möbius function values up to n
mu = ones(1, n);
for i = 2:sqrt(n)
if mu(i) == 1
for j = i^2:i:n
if mod(j, i^2) == 0
mu(j) = 0;
else
mu(j) = -mu(j);
end
end
end
end
end
As you have guessed, program number two is not correct. Even its own plot reveals that something is amiss.
Program number three
Let's return to the second Web site and make a more specific query.
Please write a MATLAB program that uses Redheffer matrices to test the Mertens conjecture.
The resulting program generates a Redheffer matrix with
R = zeros(n,n);
for i = 1:n
for j = 1:n
if mod(i, j) == 0
R(i, j) = 1;
end
end
end
It computes the determinant to obtain the Mertens value, M(n). It is able to confirm the conjecture for all the n in the given range.
What's wrong now? Look at the plot. The computed M(n) is always equal to one. Why?
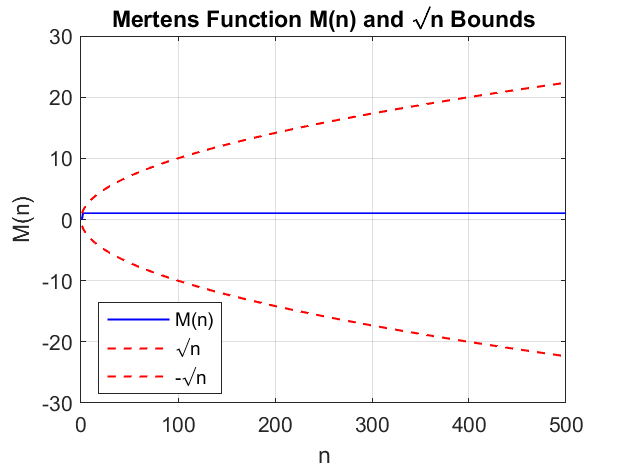
Happy Ending
Program number three can be repaired by adding one line to the code that generates R. What is that line? Respond in the comments.
Look at the good side. Instead of just using AI to do homework, we can challenge students to check the results carefully and repair any incorrect programs.
- Category:
- Algorithms,
- History,
- Programming









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.