かねてから電力会社は、発電から送電に関わる運営に対する一括した責任によって、電源開発や系統設備の導入を継続的に行って、安定的な電力の供給を担ってました。しかし、3.11の震災を機に、それ以前から議論のあった電力自由化や総括原価方式の見直しが急速に進み、2016 年からオープンな電力市場が形成されました。
さらに一部の電力会社は、発送電分離化され、発電、送電の会社へと分社化されました。当初、これらは電気料金を下げる目的で政策が施行されましたが、再生可能エネルギーの大量導入と固定価格買取制度(FIT)による需要者負担増(いわゆる再エネ賦課金)、LNGなどの燃料高騰等によってここ数年の電気料金は増加しています。
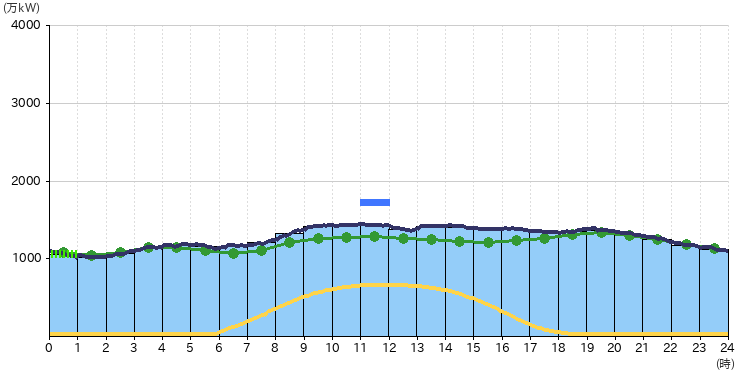
上の図は、関西地域におけるとある日の電力の実績です。電力のトレンドは各社がでんき予報として公開しています。
図中の黄色の曲線は太陽光の発電実績になりますが、見ての通り、太陽が真上にくる正午をピークとして、小高い丘のような形状をしています。日が落ちる夕方から夜間の発電実績は0[kW]です。このように再エネは気象現象によって発電できない時間帯が発生します。(注記:再エネの中でも水力や地熱は比較して安定的な電源です)
我々が消費する電気は、今消費している電力とピッタシ同じ量だけ発電することで正常に回っています。少しでも需要と供給に過不足が発生すると、系統の周波数(東は50[Hz]、西は60[Hz])がだんだんと乱れ、やがては発電機が耐え切れずに系統から続々と解列していき、ブラックアウト(大規模停電)します。ブラックアウトと言えば、北海道の例が記憶に新しいですね。(参考:
資源エネルギー庁HPより 日本初の“ブラックアウト”、その時一体何が起きたのか)
この需要と供給が完全に一致することを同時同量と呼びますが、再エネが出力をバンバン振ってしまうと系統が不安定化しやすくなります。そのため、不測の事態に備えるために、調整用の火力発電が出力を下げて、常時運転をキープしたり、細かな起動停止を行う必要が出てきます。ただし、火力発電は定格負荷で熱効率が最大になるように設計されているので、部分負荷帯で運転をすると、効率が悪くなります。
また燃料の在庫制約を考慮したり、発電の経済性を考えたりと、各発電所の運営を考えるのは至難の業です。実際、電力会社によっては100を超える発電所の運営を行っているケースもあるので、その一つ一つの計画を人間が考えるとなると作業の膨大さが容易に想像できるかと思います。
こうした発電所の運営にまつわる問題背景に対し、従来からOR(オペレーションズ・リサーチ)の技術が活用されてきました。ここで、OR とは数学や統計モデル、最適化手法を活用し、経営や運用など実社会における様々な問題に対し、ある指標に対し最も効率的になるような意思決定を行う科学的アプローチの総称です。(参考:
電力システム改革に対応した火力発電計画作成システムの最適化計算手法の開発)
実際に上記論文では、最新の OR システムの導入によって、燃料費ベースで年間 0.48% もの経済性を改善したとの報告が上がっています。仮に年間数兆円規模の燃料調達費がかかると想定すると、数十億円の規模でコストカットしている計算です。さらに環境問題となる CO2 排出量もモデル化し、OR で解く問題に取り込むことで、CO2 排出量が最も少ない発電所の運営を立案できます。これは、Math(数学)の力を活用することで実社会に対し大きな貢献ができることを示す良い例かと思います。
発電機の起動停止計画問題(Unit Commitment)
では、実際に火力発電機群の起動停止問題を解くといった場合にどうするかというと、最適化問題に定式化してソルバーによって解かせます。MATLAB の製品ファミリーであるOptimization Toolbox™ には、
発電機のスケジューリング問題の例題があるので、これをベースにちょこっと改良して、簡単な発電所のスケジューリング問題を解かせてみることにしました。
例題として、6 台の火力ユニット(石炭2基、LNG3基、石油1基)の構成で、1 日の需要予測に対し、燃料費が最も安くなる構成パターンを組み合わせ最適化問題によって解かせます。なお、問題では 1 日 24 hを 30 分毎に刻んだ時断面(メッシュ)について、計 48 メッシュにおけるユニット構成を決めていきます。
上の図は、火力ユニットに対する電力需要 [MW] を想定しており、昼間に太陽光がバンバン発電して、火力の需要が一時減ってしまうものの、夕方にかけてから太陽光の出力が減少し、再び火力の需要が一気に増加、ピークで使用率 100 %となるような厳しいパターンを想定しています。(通称 ダックカーブ、参考:
太陽光発電の増加に伴う課題「ダックカーブ現象とは」)
問題では、この需要に対し、各種運転制約(後述)を考慮しながら、同時同量の原則で最も経済的な運転パターンを決めます。
続いて、各発電機の特性は下表のとおりとします。(数値はダミー)
項目概要:
- a,b,c : MW(発電出力)に対する燃料費特性(¥)※2次関数(¥ = ax^2+bx+c)で近似
- P_MAX, P_MIN : 発電機が出力できるMWの上下限(MW)
- Start Up Cost : 発電機が停止から起動する際にかかるコスト(¥)
- Fuel : 燃料のタイプ ※石炭、LNG、石油の3種 LNGはGTCCを想定
- Minimum_Operation : 一度起動したら運転を継続しなければならない最小時間(メッシュ)
- Minimum_Stop : 一度停止したら停止を継続しなければならない最小時間(メッシュ)
さて、発電機の起動停止計画問題は、どの発電機を選択するかを0-1の2値による表現、すなわち整数で表すため、整数と発電出力 MW(実数)の両方を最適化の決定変数に含む、混合整数計画問題(Mixed Integer Programming : MIP)と呼ばれる、解くことが難しい問題(NP 困難)に帰着されます。
Optimization Toolbox™ では、この MIP に対応するソルバーとして
混合整数線形計画問題(Mixed Integer Linear Programming : MILP)を解く
intlinprog があるので、これを使って問題を解かせてみようと思います。
詳細には、MILP で解くと時間ががかることが想定されるので、グリーディ法によってユニットの仮決め(初期推定解)を行ってから、MILP によって最適なユニットの構成を決め、最後に QP(2次計画問題)によって具体的な MW を決めるという段階的なアプローチで時間の短縮を図ろうと思います。
MILPによる並解列の計算
MILP では、1 メッシュ毎(30分毎)の電力需要に対する経済的なユニットの運転状態(離散値)を決めていきます。
運転状態としては、大まかに最低出力 (P_MIN)、中間出力 ((P_MAX-P_MIN)/2)、最大出力 (P_MAX)の3つを用意します。各運転状態は0-1の設計変数として用意し、ソルバーによって選択させます。なお、Optimization Toolbox™では、最適化問題のプログラミングにおいて
問題ベースのアプローチを行うことが可能となっています。
問題ベースのプログラミングとは、要するにシンボリックな変数名(aとかxとかの記述)で最適化の定式をそのままプログラム化できるということです。たとえば、運転状態(低、中、高)を y という 0-1 の決定変数に当てはめる場合には、以下のように定義します。
nPeriods = 48; % total mesh number
nGens = 6; % total unit number
y = optimvar(‘y’,nPeriods,nGens,{‘Low’,‘Middle’,‘High’},‘Type’,‘integer’,‘LowerBound’,0,…
各ユニットが一つのメッシュで取り得る運転状態は1つであるため、以下のようにすべての総和が1以下になるという制約を考慮します。
なお、場合によっては運転状態のどれも選択しない、即ち、停止もこの制約によって加味できます。
powercons = y(:,:,‘Low’) + y(:,:,‘Middle’) + y(:,:,‘High’) <= 1;
続いて、各メッシュにおけるMWの需要に対し、必要な供給量が満足されるように不等式制約を設けます。ここで、i がメッシュ、j がユニット、k が運転状態の添え字(Lowから順に1~3)、$gen$ が $(i, j, k)$ において取り得る出力(MW)を表します。
$ MW_i \leq \sum_{k=1}^{3}\sum_{j=1}^{nGens} gen(i,j,k) + s_i$, $i=1,2,3…,48 $, $ nGens = 6 $
上式において厳密な等号としないのは、発電機の稼働を運転状態という離散化された有限のパターンの内から選択するようにしているため、厳密な出力のマッチングが保証されないためです。また不等式右辺に s という変数がありますが、これは不等式を緩和するために設けたスラック変数(非負の実数)です。
不等式を緩和する意図は、積み上げた供給力が足りないと制約が満たせなくなり、実行可能解がないという状態に陥ってしまいます。実行可能解が見つからないとしてもどこが厳しいのかを把握するためにも解を出力できる状態にしておきたいと思います。なお、スラック変数もソルバーによって選択させる決定変数なので以下のように定義します。
s = optimvar(‘s’,nPeriods,‘Type’,‘continuous’,‘LowerBound’,0); % Slack Variable
loadcons = optimineq(nPeriods,1);
loadcons(i) = sum(gen(:,1)’.*y(i,:,‘Low’) + gen(:,2)’.*y(i,:,‘Middle’) + gen(:,3)’.*y(i,:,‘High’)) + s(i) >= MW(i);
またソルバーが発電機の停止と起動をむらみやたらに選択させないように考慮します。ここで、運転状態の変数である $y(i, j, k)$ のオン1とオフ0の期間に応じて決まる補助変数 z を導入します。
z = optimvar(‘z’,nPeriods,nGens,‘Type’,‘integer’,‘LowerBound’,0,…
ソルバーが変数zを設定できるようにするには、次のように定式化します。
・条件 $z(i,j) = 1$ が厳密に $\sum_k y(i,j,k) = 0$ と $\sum_k y(i+1,j,k) = 1$ という条件下において満たされる必要がある
・$z(i,j) = 1$ が厳密に満たされる場合に、 $\sum_k (y(i+1,j,k) – y(i,j,k)) > 0$ となる
したがって、問題の定式化として次の線形不等式制約を含めます。
$ \sum_k (y(i+1,j,k) – y(i,j,k)) – z(i,j) < = 0 $
また、zは最適化の評価関数(後述)に含めるため、最小化問題を前提とするとソルバーはzに対し、その値を低くしようとします。つまり、ソルバーはすべてのz(停止から起動への変化)を0にしようとします。
しかし、需要増加によって発電機の起動が迫られるタイミングでは、線形不等式によって $ $z(i,j)$ $が 1 に等しくなるよう強制されるという具合になります。ここで利便性のために、$ $y(i+1,j,k) – y(i,j,k)$ $を表す補助変数wを作成しておきます。
w = optimexpr(nPeriods,nGens); % Allocate w
idx = 1:(nPeriods-1); % nPeriods = 48
w(idx,:) = y(idx+1,:,‘Low’) – y(idx,:,‘Low’) + y(idx+1,:,‘Middle’) – y(idx,:,‘Middle’) + y(idx+1,:,‘High’) – y(idx,:,‘High’);
w(nPeriods,:) = y(1,:,‘Low’) – y(nPeriods,:,‘Low’) + y(1,:,‘Middle’) – y(nPeriods,:,‘Middle’) + y(1,:,‘High’) – y(nPeriods,:,‘High’);
あとは最小起動時間と最小停止時間の制約を設定します。
まず最小起動時間ですが、前述のとおり一度発電機が起動したら継続しなければならない最小の運転時間になります。定式化すると次式の通りです。
$ \sum_{k=1}^{3}(y_{ijk}-y_{i-1jk}) \leq \sum_{k=1}^{3}(y_{\tau jk}) $, $ \tau = i+1,…..min(i+L_j-1,48) $, $ i = 2,3,…,48 $, $ j = 1,2,3,…,nGens(=6) $
上式においてLは各ユニットの最小起動時間(メッシュ)です。
minOpecons = optimineq(nPeriods-1,nGens,max(minOperation)); % minOperation is vector of L
for i = 2:nPeriods % nPerods = 48
for j = 1:nGens % nGens = 6
for l = 1:min(i+minOperation(j)-1,nPeriods)-(i+1)+1
minOpecons(i-1,j,l) = y(i,j,‘Low’) – y(i-1,j,‘Low’) + y(i,j,‘Middle’) – y(i-1,j,‘Middle’) + y(i,j,‘High’) – y(i-1,j,‘High’) <= y(tau,j,‘Low’) + y(tau,j,‘Middle’) + y(tau,j,‘High’);
同じ原理で、最小停止時間の制約も定式化します。最小停止時間は一度停止したら停止を継続しなければならない最小の時間です。
$ \sum_{k=1}^{3}(y_{i-1jk}-y_{ijk}) \leq \sum_{k=1}^{3}(1-y_{\tau jk}) $, $ \tau = i+1,…..min(i+l_j-1,48) $, $ i = 2,3,…,48 $, $ j = 1,2,3,…,nGens(=6) $
minStopcons = optimineq(nPeriods-1,nGens,max(minStop)); % minStop is vector of l
for l = 1:min(i+minOperation(j)-1,nPeriods)-(i+1)+1
minStopcons(i-1,j,l) = y(i-1,j,‘Low’) – y(i,j,‘Low’) + y(i-1,j,‘Middle’) – y(i,j,‘Middle’) + y(i-1,j,‘High’) – y(i,j,‘High’) <= (1-y(tau,j,‘Low’)) + (1-y(tau,j,‘Middle’)) + (1-y(tau,j,‘High’));
制約は以上で全てです。
最後に最適化の評価関数を定式化します。
評価関数は、発電機の運転時の燃料費、停止中の発電機を起動する際に生じる起動損失、スラック変数から構成します。
$ J = \sum_{k=1}^{3} \sum_{j=1}^{nGens} \sum_{i=1}^{nPeriods} f_{jk} y(i,j,k) + \sum_{j=1}^{nGens} \sum_{i=1}^{nPeriods} h_jz(i,j) + \sum_{i=1}^{nPeriods}s_i $
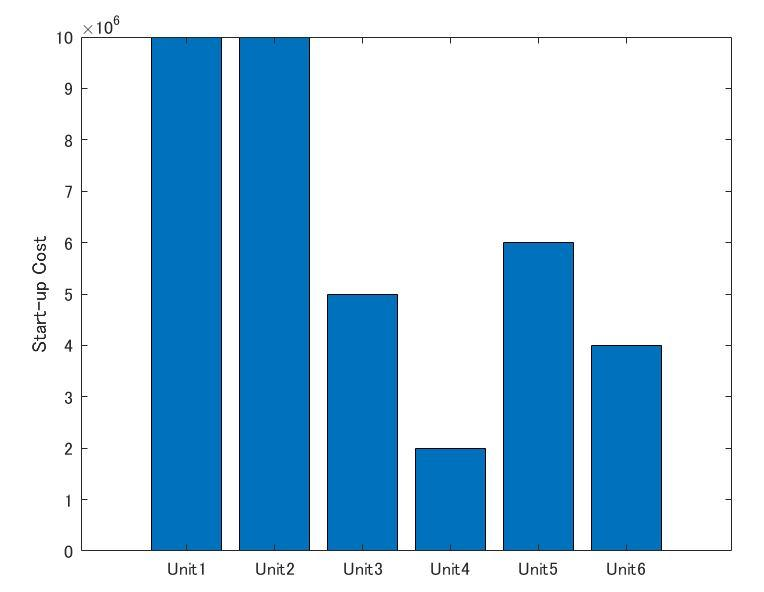
上式においてfは運転状態に応じた燃料費の特性、hは起動損失($ $z=1$ $の時に掛かってくる)です。
これをコードで書くと以下の通りです。なお、コード上では、コストの正規化処理とスラック変数を小さくするための重みをそれぞれ掛けています。
startingCost = z*startCost;
totalCost = (sum(sum(sum(fuel))) + sum(sum(startingCost)))/scaleFactor + weight_slack*sum(s);
以上でMILPの定式化が整ったので、これをソルバーに食わせて問題を解いてくれるのを待ちます。
最適化問題を設定するために専用のAPIである
optimproblemを呼び出してオブジェクトを作成し、これまで作った制約条件と評価関数を指定していきます。
unitCommit = optimproblem(‘ObjectiveSense’,‘minimize’);
unitCommit.Objective = totalCost;
unitCommit.Constraints.switchcons = switchcons;
unitCommit.Constraints.powercons = powercons;
unitCommit.Constraints.loadcons = loadcons;
unitCommit.Constraints.minOpecons = minOpecons;
unitCommit.Constraints.minStopcons = minStopcons;
最後に intlinprog のオプションを諸々設定して、solve コマンドで解きます。ここで、solve コマンドの引数に与えている unitCommit0 は初期推定解で、事前にグリーディ法で求めています。(グリーディ法は割愛)
ちなみに初期推定解を空欄([ ])にしても解かせることは可能です。
options = optimoptions(‘intlinprog’,‘Display’,‘iter’,‘CutMaxIterations’,50,‘CutGeneration’,‘advanced’,‘IntegerPreprocess’,‘advanced’,‘HeuristicsMaxNodes’,1800,‘Heuristics’,‘advanced’,‘BranchRule’,‘strongpscost’,‘MaxTime’,7200,‘ObjectiveImprovementThreshold’,1e-4,‘RootLPAlgorithm’,‘primal-simplex’);
[unitCommit,fval,exitflag,output] = solve(unitCommit,unitCommit0,‘options’,options);
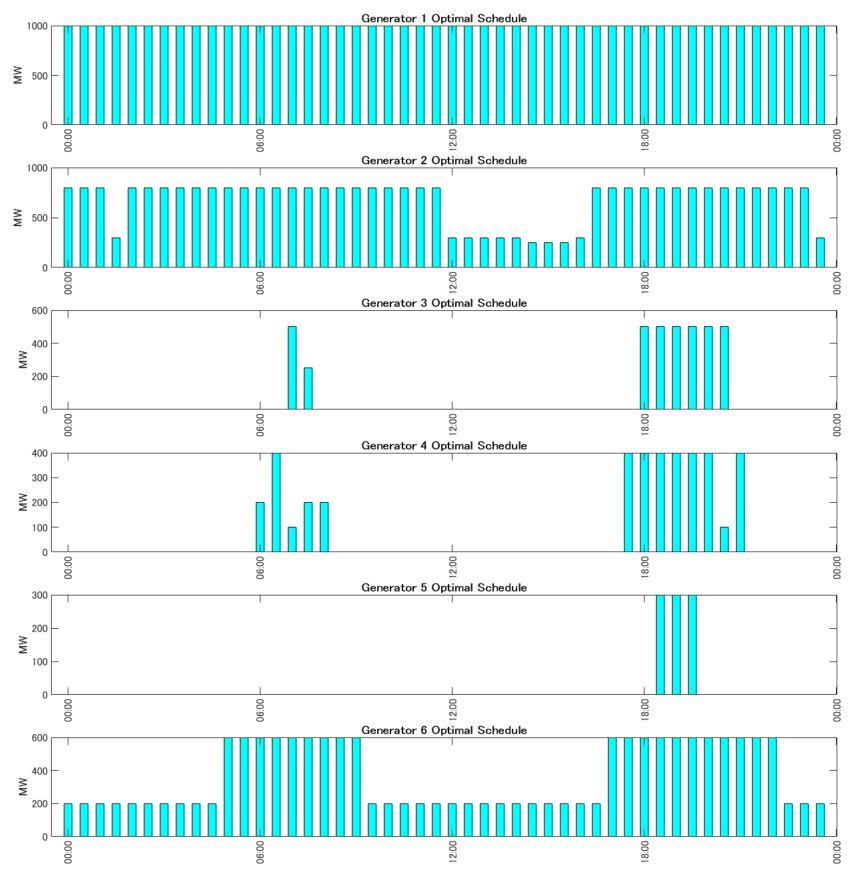
実際に実行すると以下のような結果になりました。
上図は上からユニット 1~6 と並んでいます。また各運転状態に対する燃料費の比較図とユニットごとの起動損失の比較図を以下に示します。
結果から出力が大きく、燃料費の安い石炭火力(ユニット 1,2)がベースロードでずっと運転しています。
ただ、ユニット 2 に至っては、正午で需要が下がるタイミングで出力を下げて調整を行い、需要が上がる18時を前に最大出力に戻します。また LNG で出力が大きく、比較して燃料費の抑えられるユニット 6 も負荷を調整しながら運転しています。LNGのユニット 3,4と石油のユニット5が残りの分担を行いますが、特に一日の中で起動と停止を行う、いわゆる
DSS(日間起動停止)運転を行っていることが分かります。
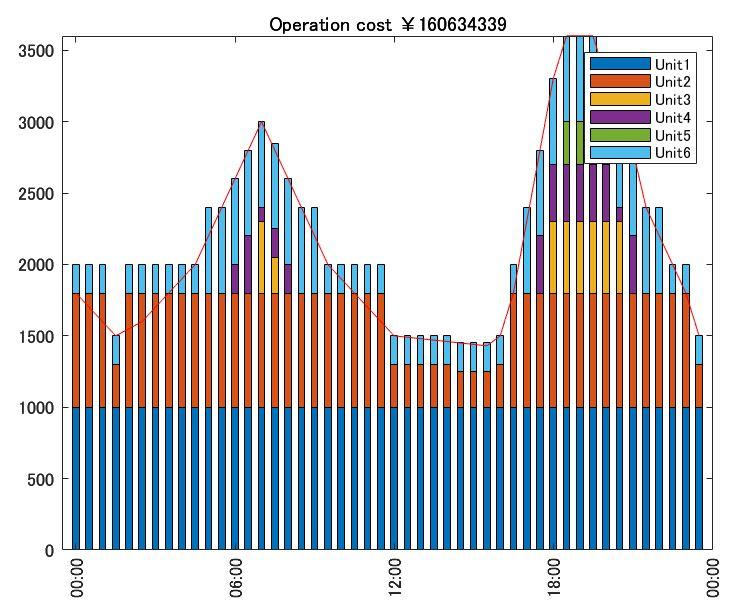
需要に対する供給力の曲線を表示すると次の通りです。
赤線で示す需要に対し、各メッシュで積み上げの供給量が同じか、上回っていることが分かります。ちなみにこのパターンでの運転費の概算は1億6063万4339円です。
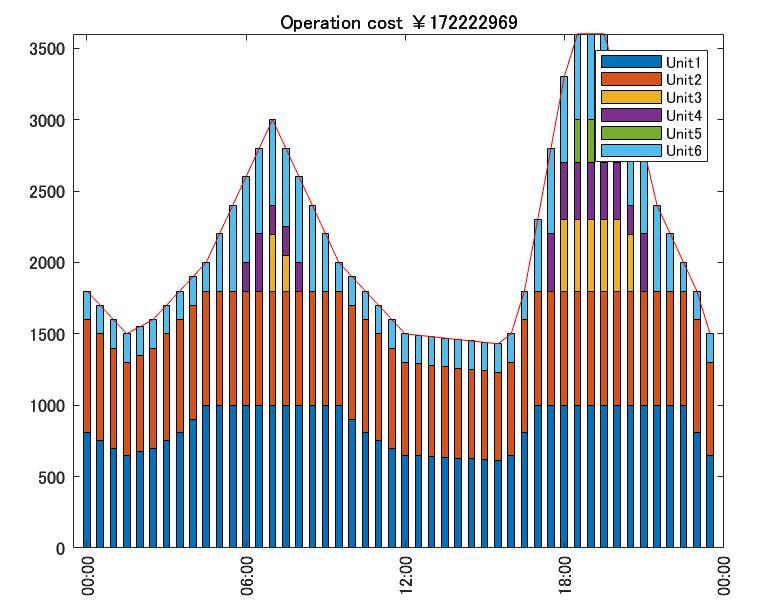
MILPによる並解列の計算で運転するユニットを決められたので、あとは完全に需要=供給力となるように各プラントの出力上下限(P_MAX,P_MIN)を考慮しながら燃料費が最小となる出力をQPによって決めます。詳細は割愛しますが、結果のみ掲載します。
結果から需要に対し、ピッタシ供給できていることが分かります。最終的な燃料費は1億7222万2969円となります。
最後に
このように発電所の運営は最適化問題として解かれます。
実際のシステムはもっと複雑で様々な運転制約や燃料在庫問題を考慮し、また作成する計画の長さも 1 年分・ 1 カ月分・1 週間分・1 日単位など様々です。普段何気なく利用している電気ですが、一部ではこのように計画し運営されています。
この冬は電力需給がかなり厳しいと予測されていますが、限りある電気を大事に使っていきたいですね。
余談 アプリ化の話
最後に作った MATLAB のコードは App Designer を使って共有アプリ化し、MATLAB Compiler™ を使ってMATLABをもっていない第三者に配布することもできます。






 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building



Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.