Inverse Mapping from Values to Indices

Contents

Tidy up to start.

clear
format short g

Sample Input and Results

Supppose I have an array a containing values that I expect to find in another array, Minit.

a = [1 3 5 7 8]
Minit = [1 3 5; ...
    3 5 7; ...
    3 7 8]

a =
     1     3     5     7     8
Minit =
     1     3     5
     3     5     7
     3     7     8

I would like to see a replacement matrix for Minit in which the values are replaced with their indices in the list a.

Mwanted = [1 2 3; ...
     2 3 4; ...
     2 4 5]

Mwanted =
     1     2     3
     2     3     4
     2     4     5

Algorithms

There are at least three ways to accomplish the task, one, a brute force loop, and two that require knowledge of other very useful MATLAB functions, histc and ismember.

Let's first look at the for-loop solution.

type loopFR

function M1 = loopFR(M,A)
% loopFR replaces M with its indices from A.

% First set up the inverse mapping array.  Initialize it to zero, and the
% size is the maximum number the array.  Note that I get away with this
% here because all of my numbers in both A and M are positive integers.
imap = zeros(1,max(A));  % inverse mapping array
% Now fill the inverse map, but placing in the location specified in each
% element of A, the index of that element in A.
% If A = [1 5 4], then imap = [1 0 0 3 2].
imap(A) = 1:length(A);  
M1 = M;
for k = 1:numel(M)
    M1(k) = imap(M(k));
end

Here, I set up imap, an array that allows me to do the inverse mapping from values in a back to indices in a.

And check that loopFR gets the right result.

isequal(loopFR(Minit,a), Mwanted)

ans =
     1

Now let's check both ismember and histc before spending effort timing the results.

[mem, mem] = ismember(Minit,a);
[his, his] = histc(Minit,a);
isequal(Mwanted, mem, his)

ans =
     1

Time the Algorithms

N = [1 10 100 1000 10000 100000];  % repetitions to test
t = zeros(length(N),3); % set up the timing collection array
for n = 1:length(N)
    % Make a larger matrix to search.
    % loopFR
    M = repmat(Minit,N(n),1);
    tic
    M1 = loopFR(M,a);
    t(n,1) = toc;
    % ismember
    tic
    [M2,M2] = ismember(M,a);
    t(n,2) = toc;
    % histc
    tic
    [M3,M3] = histc(M,a);
    t(n,3) = toc;
    if ~isequal(M1,M2,M3)
        disp('oops')
    end
end

Timing Results

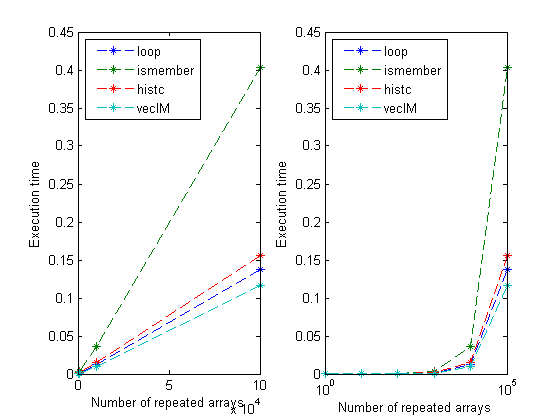
disp('       Counter     numel(M)     loop       ismember     histc')
disp([N' 9*N' t]);
subplot(1,2,1)
plot(N', t, '--*')
xlabel('Number of repeated arrays')
ylabel('Execution time')
legend({'loop','ismember','histc'},'Location', 'NorthWest')
subplot(1,2,2)
semilogx(N', t, '--*')
xlabel('Number of repeated arrays')
ylabel('Execution time')
legend({'loop','ismember','histc'},'Location', 'NorthWest')

       Counter     numel(M)     loop       ismember     histc
            1            9  4.5537e-005   0.00012627  1.2292e-005
           10           90  2.8775e-005  8.8838e-005  1.3689e-005
          100          900  6.6489e-005   0.00022042  5.8108e-005
         1000         9000   0.00046542    0.0017497   0.00051291
        10000        90000     0.004678     0.015192    0.0059801
       1e+005       9e+005     0.065959      0.20439     0.063979

Comments

Two important things to point out. First, the matrix M that I use throughout is probably not representative of such arrays as the array size grows since I created it via replication. Often in such a case, the number of unique elements in a, the inverse mapping matrix, would also grow, at least a bit. Second, I used preallocation for the loop code to make sure I didn't get a time hit from growing the array, but I was not expecting the for loop results to be so competitive with those from histc. Please add your thoughts or results below.

Published with MATLAB® 7.2