Rooting Around in MATLAB – Part 1
I've been interested in teaching for a long time, including ways to use MATLAB. One concept that students might need to understand early in their college careers is that of finding roots or zeros of functions. To understand at least some of the algorithms, you might want to teach the students about fixed points for functions. It's the basis for some methods of solving equations or finding roots, algorithms such as Newton's method, finding square roots, and more.
Contents
Example Function
Let's start with a simple cubic polynomial f.

Here's one common way to represent this polynomial in MATLAB, using coefficients of descending powers of the independent variable.
p = [1 0 1 -1];
I can then use polyval to evaluate the polynomial. And then I can plot it.
x = -2:0.1:2;
y = polyval(p,x);
plot(x,y)
title f
grid
I could also represent the polynomial as an anonymous function and plot it with fplot.
f = @(x) x.^3 + x - 1; fplot(f,[-2 2]) title f grid on

Find the Roots or Zeros
I have at least 2 choices in MATLAB for finding a zero or root of this polynomial. The first is to use roots to get all the possible zeros.
rsolution = roots([1 0 1 -1])
rsolution =
-0.34116 + 1.1615i
-0.34116 - 1.1615i
0.68233
You can see that this polynomial has one real root between 0 and 1, and 2 complex roots.
You can also use fzero, one of MATLAB's optimization functions, to find the value. Here we'll select 0.5 as the initial guess.
fzsolution = fzero(f,0.5)
fzsolution =
0.68233
In the next post, I'll describe a way to solve this same problem using an algorithm based on fixed point iteration.
The Series of Posts
In addition to this post, there will be two more. Until they are published, the following two links will not be available.



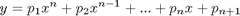




댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.