Spatial transformations: maketform, tformfwd, and tforminv
Several Image Processing Toolbox functions related to spatial transformations use "tform" structures. A tform structure has data and function handles needed for applying a spatial transformation in the forward or the inverse direction, and sometimes in both directions.
Contents
maketform
Function maketform has several syntaxes for constructing different types of tform structures. For example, you can construct an affine transform by providing an A matrix:
A = [2 0 0; 0 2 0; 0 0 1]; % Stretch by a factor of 2 in both directions. tform = maketform('affine', A);
tformfwd
Toolbox function tformfwd transforms points from input space to output space. For example, to apply the affine transform above to the point (u,v) = (2,3), do this:
uv = [2 3]; xy = tformfwd(tform, uv)
xy =
4 6
tforminv
Function tforminv transforms points from output space to input space. If we apply the inverse transformation to the point xy computed above, we should get back the original point.
uvp = tforminv(tform, xy)
uvp =
2 3
Introducing George
The spatial transformation functions imtransform, tformarray, tformfwd, tforminv, etc., were introduced to Image Processing Toolbox version 3 in 2001. While designing these functions, we almost always had input-space output-space diagrams on our whiteboards so we could keep our notation straight.
Because I have no drawing skills, I always drew a crude head-and-shoulders outline on these diagrams as the "image" being transformed. I started calling this figure "George." Here's what he looks like:
% https://blogs.mathworks.com/images/steve/37/george.mat load george plot(x,y), axis ij, axis equal, axis([-1 1 -1 1]), grid on
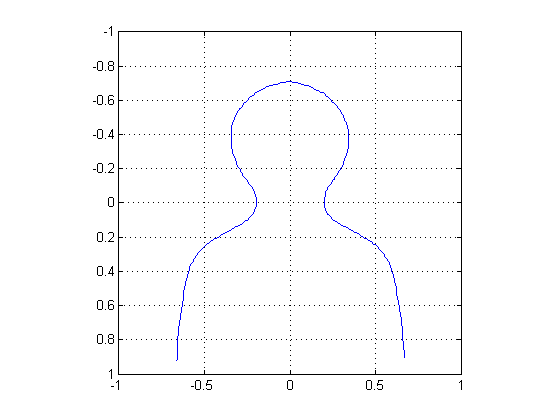
Why "George"? Well, any graduate of the Georgia Institute of Technology will recognize George's full name: George P. Burdell. If you don't know George and are curious, I'm sure Google will turn something up for you.
I like to use George to illustrate different affine transforms.
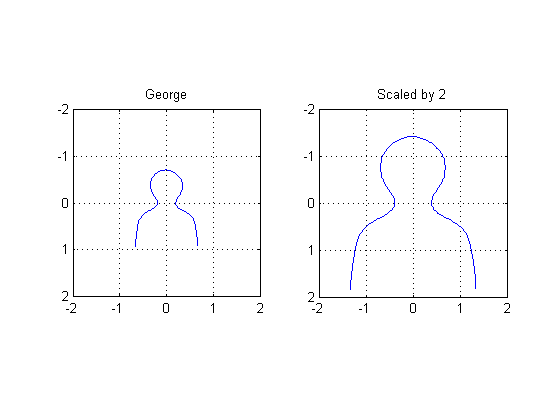
Scaling example
A1 = [2 0 0; 0 2 0; 0 0 1]; tform1 = maketform('affine', A1); uv1 = tformfwd(tform1, [x y]); subplot(1,2,1) plot(x,y), axis ij, axis equal, axis([-2 2 -2 2]), grid on, title('George') subplot(1,2,2) plot(uv1(:,1), uv1(:,2)), axis ij, axis equal, axis([-2 2 -2 2]) grid on title('Scaled by 2')
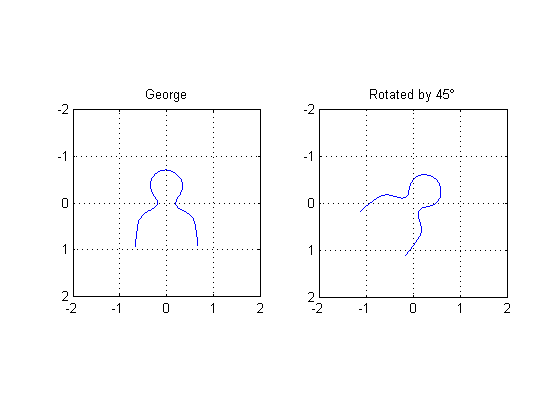
Rotation example
theta = pi/4; A2 = [cos(theta) sin(theta) 0; -sin(theta) cos(theta) 0; 0 0 1]; tform2 = maketform('affine', A2); uv2 = tformfwd(tform2, [x y]); subplot(1,2,1) plot(x,y), axis ij, axis equal, axis([-2 2 -2 2]), grid on, title('George') subplot(1,2,2) plot(uv2(:,1), uv2(:,2)), axis ij, axis equal, axis([-2 2 -2 2]) grid on title('Rotated by 45\circ')
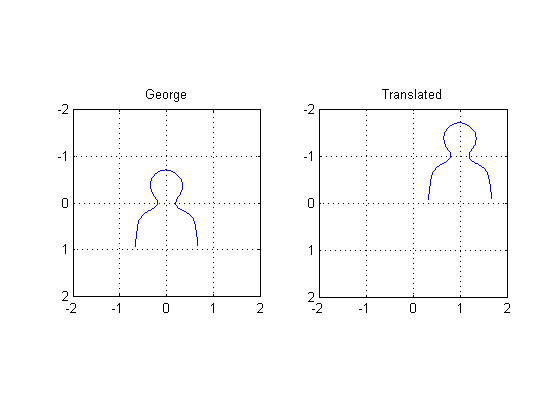
Translation example
A3 = [1 0 0; 0 1 0; 1 -1 1]; tform3 = maketform('affine', A3); uv3 = tformfwd(tform3, [x y]); subplot(1,2,1) plot(x,y), axis ij, axis equal, axis([-2 2 -2 2]), grid on, title('George') subplot(1,2,2) plot(uv3(:,1), uv3(:,2)), axis ij, axis equal, axis([-2 2 -2 2]) grid on title('Translated')
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.