Contents

maketform

Function maketform has several syntaxes for constructing different types of tform structures. For example, you can construct an affine transform by providing an A matrix:

A = [2 0 0; 0 2 0; 0 0 1];  % Stretch by a factor of 2 in both directions.
tform = maketform('affine', A);

tformfwd

Toolbox function tformfwd transforms points from input space to output space. For example, to apply the affine transform above to the point (u,v) = (2,3), do this:

uv = [2 3];
xy = tformfwd(tform, uv)

xy =

     4     6

tforminv

Function tforminv transforms points from output space to input space. If we apply the inverse transformation to the point xy computed above, we should get back the original point.

uvp = tforminv(tform, xy)

uvp =

     2     3

Introducing George

The spatial transformation functions imtransform, tformarray, tformfwd, tforminv, etc., were introduced to Image Processing Toolbox version 3 in 2001. While designing these functions, we almost always had input-space output-space diagrams on our whiteboards so we could keep our notation straight.

Because I have no drawing skills, I always drew a crude head-and-shoulders outline on these diagrams as the "image" being transformed. I started calling this figure "George." Here's what he looks like:

% https://blogs.mathworks.com/images/steve/37/george.mat
load george
plot(x,y), axis ij, axis equal, axis([-1 1 -1 1]), grid on

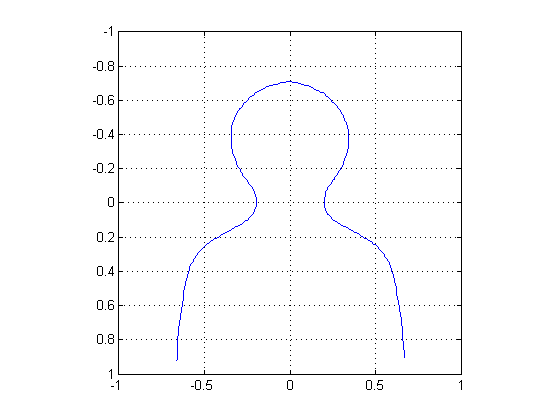
Why "George"? Well, any graduate of the Georgia Institute of Technology will recognize George's full name: George P. Burdell. If you don't know George and are curious, I'm sure Google will turn something up for you.

I like to use George to illustrate different affine transforms.

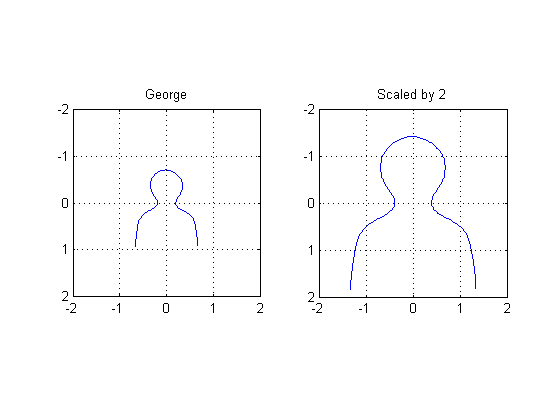
Scaling example

A1 = [2 0 0; 0 2 0; 0 0 1];
tform1 = maketform('affine', A1);
uv1 = tformfwd(tform1, [x y]);

subplot(1,2,1)
plot(x,y), axis ij, axis equal, axis([-2 2 -2 2]), grid on, title('George')

subplot(1,2,2)
plot(uv1(:,1), uv1(:,2)), axis ij, axis equal, axis([-2 2 -2 2])
grid on
title('Scaled by 2')

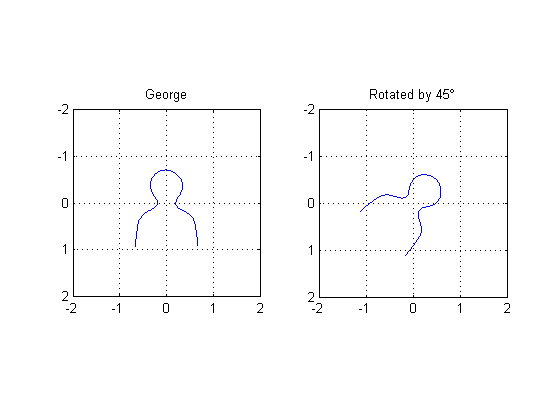
Rotation example

theta = pi/4;
A2 = [cos(theta) sin(theta) 0; -sin(theta) cos(theta) 0; 0 0 1];
tform2 = maketform('affine', A2);
uv2 = tformfwd(tform2, [x y]);

subplot(1,2,1)
plot(x,y), axis ij, axis equal, axis([-2 2 -2 2]), grid on, title('George')

subplot(1,2,2)
plot(uv2(:,1), uv2(:,2)), axis ij, axis equal, axis([-2 2 -2 2])
grid on
title('Rotated by 45\circ')

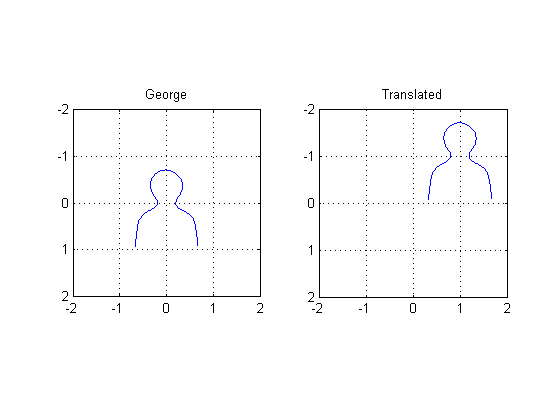
Translation example

A3 = [1 0 0; 0 1 0; 1 -1 1];
tform3 = maketform('affine', A3);
uv3 = tformfwd(tform3, [x y]);

subplot(1,2,1)
plot(x,y), axis ij, axis equal, axis([-2 2 -2 2]), grid on, title('George')

subplot(1,2,2)
plot(uv3(:,1), uv3(:,2)), axis ij, axis equal, axis([-2 2 -2 2])
grid on
title('Translated')

Get the MATLAB code

Published with MATLAB® 7.1