A Lab-based uniform color scale
DSP Tips & Tricks
One of my favorite professional publications is IEEE Signal Processing Magazine. It has a regular feature called "DSP Tips & Tricks." In the January 2006 issue, James McNames wrote a tips & tricks article called "An Effective Color Scale for Simultaneous Color and Gray-Scale Publications." Professor McNames, of Portland State University, wrote that while "color is increasingly available for electronic publications at no additional cost ... most color scales are distored when converted to gray scale. [... This] article proposes a color scale that appears as a monotonic gray scale in printed form and significantly enhances the image resolution when viewed in color."
McNames gives four design principles for selecting an effective color scale (or colormap, in MATLAB terminology):
- "[The] color scale should cover as much of the range of available colors as possible, subject to the constraint that the luminance increases monotonically (for gray scale publications).
- "Neighboring colors throughout the scale should be as distinct as possible."
- "The perceptual difference between two colors should be approximately proportional to the difference between their positions along the color scale."
- "The color scale should be intuitive."
The article goes on to show some math and some MATLAB code for creating such a color scale. Professor McNames provides a full MATLAB implementation of the idea (ColorSpiral.m) on his web site.
A path through L*a*b* color space
The McNames article describes a method for constructing a path through RGB space that has the desired properties, at least approximately. I thought it might be conceptually simpler to form a color scale by constructing a path through a different color space, L*a*b*. This color space separates luminance, L*, from two color difference components, a* and b*.
If you convert a* and b* to polar coordinates, the angle corresponds to hue, and the radius corresponds to chroma, or vividness of hue.
Let's make a color scale that is a uniform ramp in L*. In the a*-b* plane, trace a semicircular path of radius 50, with angle varying between 0 and pi/2.
radius = 50; theta = linspace(0, pi/2, 256).'; a = radius * cos(theta); b = radius * sin(theta); L = linspace(0, 100, 256).'; Lab = [L, a, b];
Now convert the L*a*b* values to sRGB so we can use it as a MATLAB colormap. Use the Image Processing Toolbox functions makecform and applycform.
map = applycform(Lab, makecform('lab2srgb'));Radon example
Let's use this colormap for looking at a Radon transform image.
I = zeros(100,100); I(25:75, 25:75) = 1; theta = 0:180; [R,xp] = radon(I,theta); imshow(R,[],'InitialMagnification','fit') colormap(map)
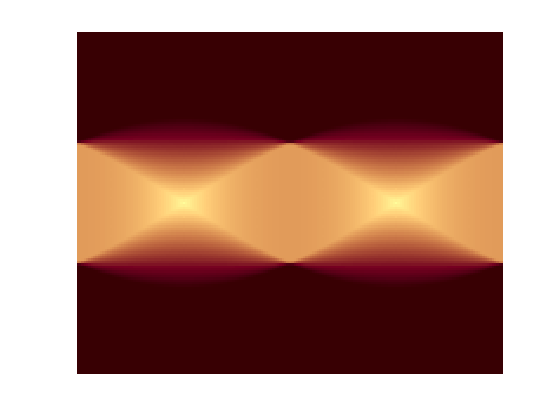
Color scale function on MATLAB Central
The function color_scale on MATLAB Central lets you easily create color scales like this. You can choose different values for the radius and the starting angle, and you specify a clockwise or counterclockwise path through a*-b* space.
colormap(color_scale)
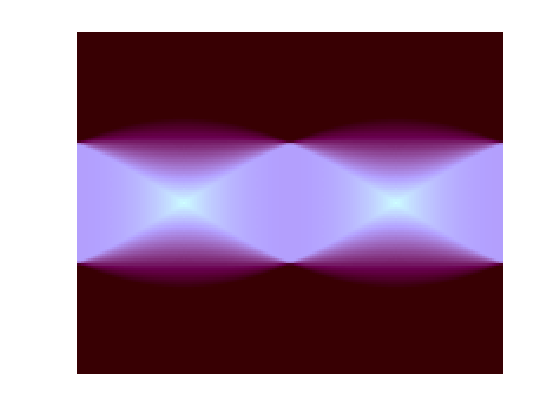
Color scale GUI
The same MATLAB Central submission contains the color_scale_tool function, which is a GUI that lets you control the color scale parameters with sliders. It also shows you both the color scale and the approximate grayscale equivalent. Here's a screen shot:
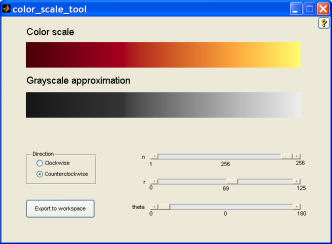
Give it a try.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.