Didja know? You can fill holes, or pits, in grayscale images by using the Image Processing Toolbox function imfill.
The other day I was rereading the Tarboton paper on upslope area, trying to decide what to do next in my series on that topic. I noticed that the author described filling in "pits" in digital elevation models (DEMs) as a common preprocessing step. He outlined a method based on pixel flow directions, but didn't give details. I realized that this preprocessing step is very easy to do using the Image Processing Toolbox, but that many users might not know about this capability.
Let me first define a little more precisely what I mean by "pit" or "hole," and then I'll show you how to fill it in. It's a little easier to show in one dimension, so let's start there.
Here's a one-dimensional function:
t = linspace(0, 3*pi, 100); y = t/2 + sin(t); plot(t,y)
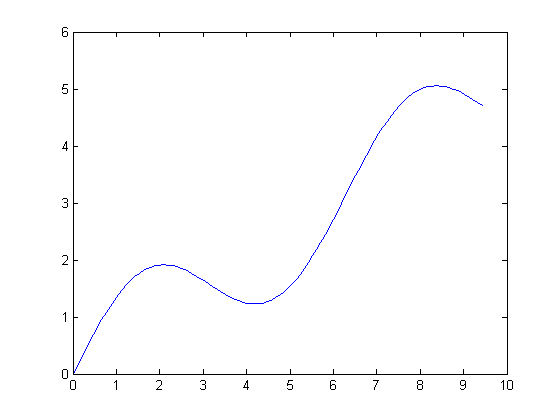
The plot above has a local minimum in its interior. This is a hole, or pit. If we are careful to define our connectivity appropriately for one dimension, we can use imfill with the 'holes' option to fill in the hole.
% Define a one-dimensional connectivity in the horizontal direction. conn = [0 0 0; 1 1 1; 0 0 0]; y2 = imfill(y, conn, 'holes'); plot(t,y2)
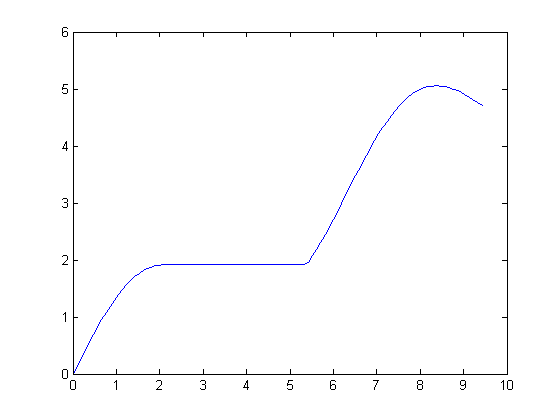
The filled curve has this key property: From any interior point, you can now travel to a boundary minimum without ever going uphill. Here's what it looks for an image:
I = imread('tire.tif'); I2 = imfill(I,'holes'); % the default connectivity is fine subplot(1,2,1) imshow(I) title('Original image') subplot(1,2,2) imshow(I2) title('Filled image')
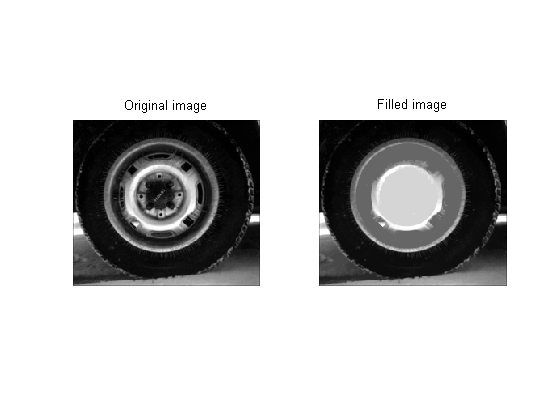
The hole-filling algorithm in imfill is based on morphological reconstruction (imreconstruct). If you are interested in the theoretical details, see section 6.3.7 of Morphological Image Analysis: Principles and Applications, 2nd ed., Springer, by P. Soille.
Get
the MATLAB code
Published with MATLAB® 7.4
Thank Steve. imfill solves my problem on removing noise inside object caused by camera flash
Hi Steve
I have an image 480×640 and i want to put in the center a black circle. Is posible if i generate the cicrle in this form?
t = imspace(0,2*pi, 100);
h=0;
k=0;
r=10;
x=r*cos(t)+k;
y=r*sin(t)+k;
plot(x,y), fill(x,y,’k');
axis square;
or i have to superimpose other image with a black circle?
thanks
i have to correct
t=linspace(0,2*pi,100);
thanks
Hilda—It depends on what you want. Do you want a single image whose center pixels in a circular region have been replaced by black pixels? Do you want to superimpose one image over another in semitransparent fashion? Do you want to superimpose a black circular patch over your image? That’s what your code looks like it’s doing. You’ll need to call:
after displaying your image and before calling fill.
hi steve .
you want to superimpose one image over another
i use the code
image(X1);
hold on;
image(X2);
but i want the second image to be at the “center” of the first.
please help
thankx..
Amal—Look at the XData and YData properties of the image object. By setting those properties you can control where an image appears.
hi Steve,
I am having trouble getting this to work in 3d:
BW1 = logical([1 0 0 0 0 0 0 0
1 1 1 1 1 0 0 0
1 0 0 0 1 0 1 0
1 0 0 0 1 1 1 0
1 1 1 1 0 1 1 1
1 0 0 1 1 0 1 0
1 0 0 0 1 0 1 0
1 0 0 0 1 1 1 0]);
BW2 = imfill(BW1,[3 3],8)
for i = 1:8
BW13(:,:,i)=BW1;
end
BW133= imfill(BW13,[3 3 3],6)
in Matlab 7.3 I keep getting errors, but it seems logical given the help documentation.
??? Function IMFILL expected its third input, OPTION,
to be one of these types:
char
Instead its type was double.
Error in ==> iptcheckstrs at 40
iptcheckinput(in, {’char’}, {’row’}, function_name, variable_name, …
Error in ==> imfill>parse_inputs at 249
iptcheckstrs(varargin{3}, {’holes’}, mfilename, ‘OPTION’, 3);
Error in ==> imfill at 124
[I,locations,conn,do_fillholes] = parse_inputs(varargin{:});
Dan—It works for me using R2007b. Be sure that the class of BW13 is logical before your last call to imfill.