Steve on Image Processing

One of the discrete-time Fourier transform properties that many people learn is that if a sequence is conjugate symmetric, 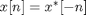, then the Fourier transform is real.

Therefore it surprises people sometimes when the output of fft is unexpectedly complex. For example:

x = [1 2 3 2 1]

x =

     1     2     3     2     1

The sequence above appears to be symmetric, but the output of fft(x) is complex:

fft(x)

ans =

   9.0000            -2.1180 - 1.5388i   0.1180 + 0.3633i   0.1180 - 0.3633i  -2.1180 + 1.5388i

So what's going on? Well, the fft function is computing the discrete Fourier transform of a sequence that is nonzero over the interval . Here's a plot:

You can see that in fact isn't actually symmetric about the origin: . is a shifted version of a symmetric sequence, and that shift causes the output of fft to be complex.

This is the symmetric sequence that has a real-valued Fourier transform:

So how do we compute the real-valued Fourier transform of that sequence using the fft function? If you'll allow me to be a bit hand-wavy here, I'll just say that the discrete Fourier transform has an implicit periodicity in both the time domain and in the frequency domain. Related to this periodicity, many of the discrete Fourier transform analogs to the more familiar Fourier transform properties involve circular shifts, or modulo indexing.

For example, the conjugate symmetry property for the discrete Fourier transform looks like this: if 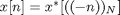, then the DFT is real. What we want to do, then, is circularly shift x so that the center element moves to the left of the vector, like this:

xs = circshift(x,[0 -2])

xs =

     3     2     1     1     2

Now take the DFT of xs:

fft(xs)

ans =

    9.0000    2.6180    0.3820    0.3820    2.6180

Now the output is real, as expected.

If you're going to zero-pad, do that first and then apply the circular shift.

x128 = x;
x128(128) = 0;
x128s = circshift(x128,[0 -2]);
X128 = fft(x128s);
isreal(X128)

ans =

     0

Whoops. Was I wrong about using this procedure to produce a real result? Not really, it's just our old friend floating-point round-off error. Look how small the imaginary part is:

max(abs(imag(X128(:))))

ans =

  4.4409e-016

You can get rid of the negligible imaginary part by using real. Let's plot the real-valued Fourier transform. I'll use the frequency axis labeling technique I showed in my June 25 blog post.

w = unwrap(fftshift(2*pi * (0:(128-1)) / 128) - 2*pi);
plot(w/pi, fftshift(real(X128)))
xlabel('radians / \pi')

Get the MATLAB code

Published with MATLAB® 7.10