Today I'm combining my blog post with a new problem submission on Cody. The problem is related to the function bwboundaries in the Image Processing Toolbox. This function traces the boundaries of objects (and holes within objects), returning each boundary as a set of x-y vertices.

Here's an example from the documentation:

I = imread('rice.png');
BW = im2bw(I, graythresh(I));
[B,L] = bwboundaries(BW,'noholes');
imshow(label2rgb(L, @jet, [.5 .5 .5]))
hold on
for k = 1:length(B)
    boundary = B{k};
    plot(boundary(:,2), boundary(:,1), 'w', 'LineWidth', 2)
end
hold off

I have heard a few times from customers that they would like to eliminate "unnecessary vertices" in the output of bwboundaries. To illustrate, let's look at the boundary for a simple binary image containing a rectangle.

close(gcf)
bw = false(15,40);
bw(5:10,10:30) = true;
B = bwboundaries(bw);
boundary = B{1};
imshow(bw,'InitialMagnification', 'fit')
hold on
plot(boundary(:,2), boundary(:,1))
plot(boundary(:,2), boundary(:,1), '*')
hold off

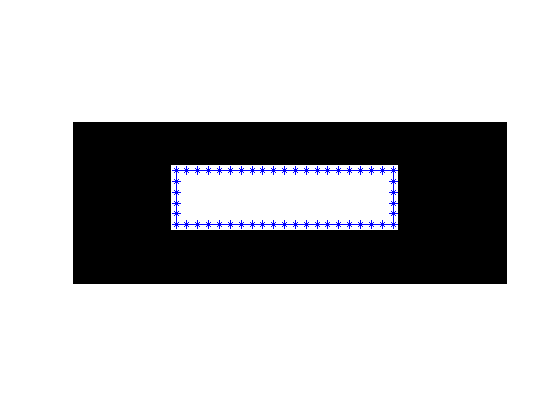
Note that the boundary goes through the pixel centers, which is why a little bit of white appears outside the boundary line.

I can imagine that for some applications it would be nice to have the boundary polygon without as many vertices, like this:

x = [10 30 30 10 10];
y = [5 5 10 10 5];
imshow(bw,'InitialMagnification', 'fit')
hold on
plot(x, y)
plot(x, y, '*')
hold off

This idea has been on my potential blog topics list for a long time, and today I finally got around to thinking about it. I can think of several different approaches, and it's not immediately obvious to me which approach might be best (for whatever definition of best you believe in).

So I thought I would make a Cody problem out of it and see what creative ideas pop up.

I encourage you to give the problem a try. I'll summarize the results later.

Good luck!

UPDATE: In a week or so, I'll a pick the best solution (according to the well-known purple-seven multiphasic optimality criterion) and send out a prize (a hat or something similar) to the solver.

Get the MATLAB code

Published with MATLAB® 7.14

Published with MATLAB® 7.14