Revisiting dctdemo – part 3
This is the third part of my plan to rewrite an Image Processing Toolbox example from 20 years ago using more modern MATLAB language features. I got the idea from Dave Garrison's recent article on writing MATLAB apps.
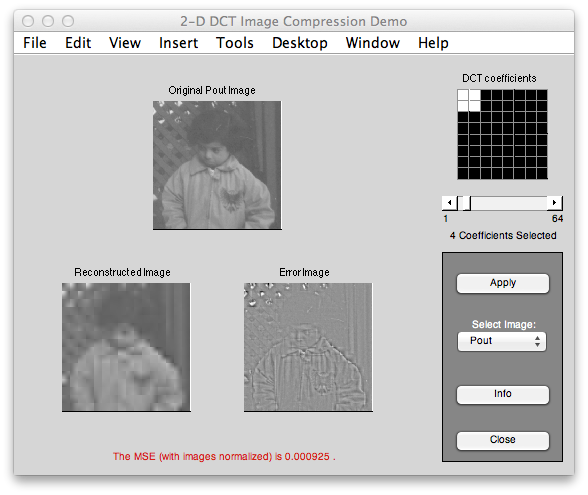
Here's the old app I'm trying to reinvent:
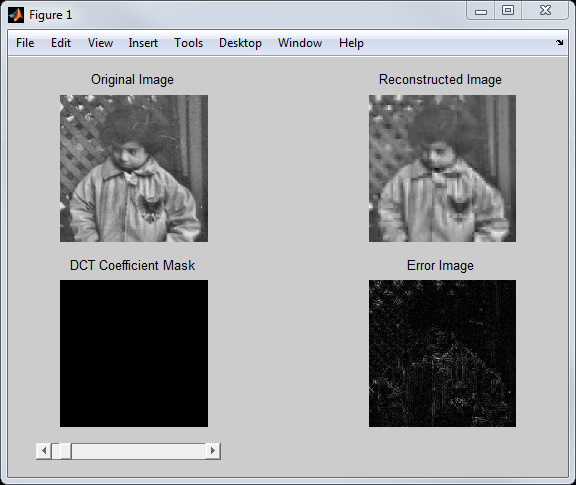
And here's what I had working the last time:

The code isn't doing any actual DCT computations yet. The idea is to compute 8-by-8 block DCTs, zero out the least significant DCT coefficients of each block, and then reconstruct the image by computing the inverse DCT of each 8-by-8 block.
Let me show how this will work on the sample image I'm using for the app:
pout = imread('pout.tif');
pout2 = pout(1:240,:);
I = im2double(adapthisteq(pout2));
imshow(I)

First, use blockproc to compute the 8-by-8 2-D DCTs.
f = @(block) dct2(block.data);
A = blockproc(I,[8 8],f);
imshow(A,[])
title('DCT coefficients')

Second, I want to compute the variances of each of the 64 coefficients. That is, compute the variance of the (1,1) DCT coefficients from each block, the variance of the (1,2) DCT coefficients from each block, and so on. I'll use the computed variances to determine which DCT coefficients to keep and which to zero out. To do this, I'll rearrange the elements from the previous step so that the corresponding DCT coefficients are together in the columns of a 64-column matrix.
B = im2col(A,[8 8],'distinct')'; vars = var(B); plot(vars) title('Variances of the 64 DCT coefficients')

Next, suppose we want to keep the 3 block DCT coefficients with the highest variances. I'll use sort to figure out which ones to keep.
[~,idx] = sort(vars,'descend');
keep = idx(1:3)
keep =
1 9 2
For an 8-by-8 block of DCT coefficients, index values 1, 9, and 2 correspond to the upper-left DCT coefficient and the two coefficients just the right and down from it. Let's keep just those coefficients.
B2 = zeros(size(B)); B2(:,keep) = B(:,keep);
Now I'll rearrange the columns back into blocks and reconstruct the image by computing the inverse DCT of each block.
C = col2im(B2',[8 8],size(I),'distinct'); finv = @(block) idct2(block.data); D = blockproc(C,[8 8],finv); imshow(D) title('Image reconstructed from 3 DCT coefficients per block')

This algorithm code into a local function to go at the bottom of my app code file, like this:
function I2 = reconstructImage(I,n) % Reconstruct the image from n of the DCT coefficients in each 8-by-8 % block. Select the n coefficients with the largest variance across the % image.
% Compute 8-by-8 block DCTs. f = @(block) dct2(block.data); A = blockproc(I,[8 8],f);
% Compute DCT coefficient variances and decide % which to keep. B = im2col(A,[8 8],'distinct')'; vars = var(B); [~,idx] = sort(vars,'descend'); keep = idx(1:n);
% Zero out the DCT coefficients we are not keeping. B2 = zeros(size(B)); B2(:,keep) = B(:,keep);
% Reconstruct image using 8-by-8 block inverse % DCTs. C = col2im(B2',[8 8],size(I),'distinct'); finv = @(block) idct2(block.data); I2 = blockproc(C,[8 8],finv); end
I already have an update method in my class, so I can add code to that method that will compute the reconstructed image and error image. Here's the revised update method:
function update(app)
recon_image = reconstructImage(app.OriginalImage, ...
app.NumDCTCoefficients);diff_image = imabsdiff(app.OriginalImage, recon_image);
imshow(app.OriginalImage,'Parent',app.OriginalImageAxes);
title(app.OriginalImageAxes,'Original Image'); imshow(recon_image,'Parent',app.ReconstructedImageAxes);
title(app.ReconstructedImageAxes,'Reconstructed Image'); imshow(diff_image,[],'Parent',app.ErrorImageAxes);
title(app.ErrorImageAxes,'Error Image'); imshow(zeros(size(app.OriginalImage)),'Parent',app.MaskAxes);
title(app.MaskAxes,'DCT Coefficient Mask');
drawnow;
endAlthough I don't have all the interactive behavior wired up yet, and don't have the DCT coefficient mask visualization done yet, the app runs and looks a bit more finished than it did before. It now shows the results for reconstructing the image from 3 DCT coefficients per block.
I think it'll take just one more post to finish making the rest of this app work.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.