Minimum Feret Diameter

Posted by Steve Eddins, February 20, 2018

25 views (last 30 days) | 0 Likes | 3 comments

Last time (if you can remember that long ago), I talked about how to find the maximum Feret diameter of a shape. The Feret diameter, sometimes called the caliper diameter, is illustrated by the diagram below. In a virtual sense, place the object to be measured inside the jaws of a caliper, with the caliper oriented at a specified angle. Close the jaws tightly on the object while maintaining that angle. The distance between the jaws is the Feret diameter at that angle.

In the last post, I demonstrated how to find all the antipodal vertex pairs of a shape, which is a useful step in finding the maximum Feret diameters of a shape.

Here is a convex shape with all of the antipodal vertex pairs shown.

It turns out that the minimum Feret diameter can also be found by looking at these antipodal pairs. Furthermore, it happens that the minimum-distance Feret calipers touch the shape at three of these vertices. I'm not going to try to prove that here, but let me illustrate it with a couple of diagrams.

Here is a shape with a couple of "caliper lines" drawn at -30 degrees. (Note that the y-axis is reversed; that's why the angle is negative.)

hull = [
    2.5000    5.5000
    3.5000    4.5000
    6.5000    2.5000
    9.5000    1.5000
   10.5000    1.5000
   10.5000    3.5000
    9.5000    5.5000
    5.5000    7.5000
    2.5000    7.5000
    2.5000    5.5000  ];

plot(hull(:,1),hull(:,2),'r','LineWidth',2)
axis equal
axis ij
axis([0 15 0 10])
hold on
plot(hull(:,1),hull(:,2),'r*')
[x1,y1] = fullLine(gca,[9.5 5.5],-30);
[x2,y2] = fullLine(gca,[6.5 2.5],-30);
caliper_lines(1) = plot(x1,y1,'k');
caliper_lines(2) = plot(x2,y2,'k');
hold off

You can always rotate these two caliper lines, by the same angle, until at least one of them touches the next antipodal vertex. When you do that rotation, the distance between the lines shrinks.

set(caliper_lines,'Color',[0.8 0.8 0.8]);
[x3,y3] = fullLine(gca,[9.5 5.5],thetad);
[x4,y4] = fullLine(gca,[6.5 2.5],thetad);
hold on
plot(x3,y3,'k')
plot(x4,y4,'k')
hold off

The Feret diameter at that rotated angle, then, is the height of the triangle formed by the three vertices, with the base of the triangle defined by the two vertices touched by the same caliper line.

delete(caliper_lines);
hold on
plot([5.5 9.5 6.5 5.5],[7.5 5.5 2.5 7.5],'Color','b','LineWidth',2)
hold off

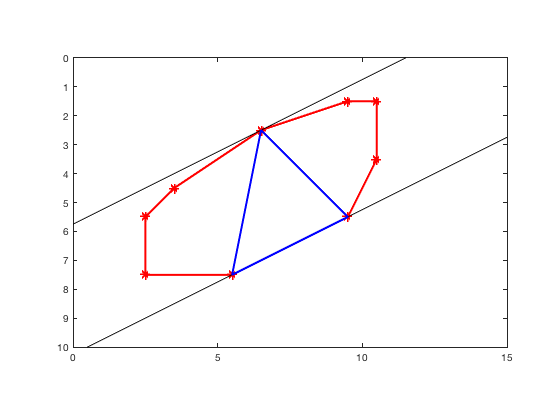
The function minFeretDiameter, which appears at the end of this post, simply walks around the set of adjacent-vertex triangles formed from antipodal vertex pairs, looking for the triangle with the minimum height.

Let's look for the minimum Feret diameter in a slightly more interesting shape.

load shape
plot(bx,by,'LineWidth',1)
axis equal
axis ij
axis([0 650 0 650])

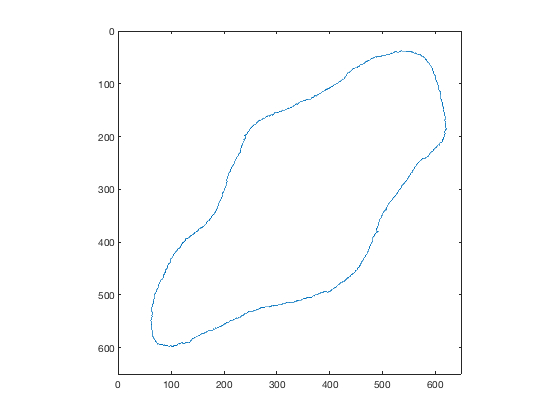
Find the convex hull, making sure to simplify it, and then find the antipodal pairs. (I showed the function antipodalPairs in my previous post.)

hull = convhull(bx,by,'Simplify',true);
S = [bx(hull) by(hull)];
pairs = antipodalPairs(S);

Now we can call minFeretDiameter.

[d,tri_points] = minFeretDiameter(S,pairs)

d =

  318.7890


tri_points =

   613   211
   459   443
   239   198

Superimpose the minimum-height triangle that minFeretDiameter found.

tri_points = [tri_points; tri_points(1,:)];
hold on
plot(tri_points(:,1),tri_points(:,2),'LineWidth',2)
hold off

Now calculate the caliper angle so that we can visualize the parallel lines of support corresponding to the minimum diameter.

dx = tri_points(2,1) - tri_points(1,1);
dy = tri_points(2,2) - tri_points(1,2);
angle = atan2d(dy,dx);
[x5,y5] = fullLine(gca,tri_points(1,:),angle);
[x6,y6] = fullLine(gca,tri_points(3,:),angle);

hold on
plot(x5,y5,'k')
plot(x6,y6,'k')
hold off

For next time, I'm tentatively planning to put together some of these concepts and use them to compute the minimum bounding box for an object.

function [x,y] = fullLine(ax,point,angle_degrees)
% Steve Eddins


limits = axis(ax);
width = abs(limits(2) - limits(1));
height = abs(limits(4) - limits(3));
d = 2*hypot(width,height);
x1 = point(1) - d*cosd(angle_degrees);
x2 = point(1) + d*cosd(angle_degrees);
y1 = point(2) - d*sind(angle_degrees);
y2 = point(2) + d*sind(angle_degrees);
x = [x1 x2];
y = [y1 y2];
end

function [d,triangle_points] = minFeretDiameter(V,antipodal_pairs)
% Steve Eddins


if nargin < 2
    antipodal_pairs = antipodalPairs(V);
end

n = size(antipodal_pairs,1);
p = antipodal_pairs(:,1);
q = antipodal_pairs(:,2);

d = Inf;
triangle_points = [];

for k = 1:n
    if k == n
        k1 = 1;
    else
        k1 = k+1;
    end

    pt1 = [];
    pt2 = [];
    pt3 = [];

    if (p(k) ~= p(k1)) && (q(k) == q(k1))
        pt1 = V(p(k),:);
        pt2 = V(p(k1),:);
        pt3 = V(q(k),:);

    elseif (p(k) == p(k1)) && (q(k) ~= q(k1))
        pt1 = V(q(k),:);
        pt2 = V(q(k1),:);
        pt3 = V(p(k),:);
    end

    if ~isempty(pt1)
        % Points pt1, pt2, and pt3 form a possible minimum Feret diameter.
        % Points pt1 and pt2 form an edge parallel to caliper direction.
        % The Feret diameter orthogonal to the pt1-pt2 edge is the height
        % of the triangle with base pt1-pt2.

        d_k = triangleHeight(pt1,pt2,pt3);
        if d_k < d
            d = d_k;
            triangle_points = [pt1; pt2; pt3];
        end
    end
end
end