CHEBFUN, Snake
Chebfun revives a classic video game, with a few mathematical twists (literally)
This is the third part of my series on Chebfun. Part one is here.
Contents
Snake
Before Angry Birds, before Tetris, even before Pac-Man, there was Snake. Around 1979 I enjoyed playing Snake on the same "glass teletype" terminal I was using to develop MATLAB. Since then, Snake has apparently been popular on cell phones, although I've never tried it there. Now, thanks to Stefan Guttel and the rest of the Chebfun team, a version of Snake with some new mathematical twists (literally) is available as part of the Chebfun distribution.
Cursor control

In the late 1970s and early '80s, between the punched card era and the PC era, we did most of our computing on time-shared main frames and minicomputers. Our favorite machine was the Digital Equipment Corporation (DEC) VAX 780, running Berkeley UNIX. We usually communicated with these machines using a DEC VT100 terminal, or some other terminal emulating a VT100.
The VT100 in the picture above looks like it could be a small computer, but it wasn't. It would be a few years before IBM, Apple and many others would make computers that small. The VT100 was just a kind of small black and white cathode ray TV set that could just display text, no graphics. There were usually 24 lines of 80 characters, although there was a mode with 14 lines of 132 characters that was hard to read and so rarely used. The 80 character line length came from punched cards and I still like to use 80 character lines in my MATLAB code today.
Video terminals were, of course, much faster than the teletypes and electric typewriters that they replaced. But for the purposes of today's blog, their most important feature was cursor control. The "escape" character, ESC, ASCII hex 1B, could be followed any of several other control characters that were not text, but that would affect the behavior of the terminal. In particular, the cursor could be moved up or down, left or right, or to any position on the screen.
Cursor control made "snake", as well as "vi", the text editor that I am using to write this blog, possible. Snake and vi were distributed with Berkeley Unix beginning in 1978 or 1979 and I started to use both of them as soon as I saw them. I guess that the novelty of snake eventually wore off, but I've been using vi ever since. Now I'm excited to see snake reappear, with some new mathematical twists.
Chebsnake
Cursor control with escape characters can now be replaced by MATLAB plot commands. Our first plot shows a typical starting configuration. The blue snake starts with only four nodes. The magenta diamond is snake food.
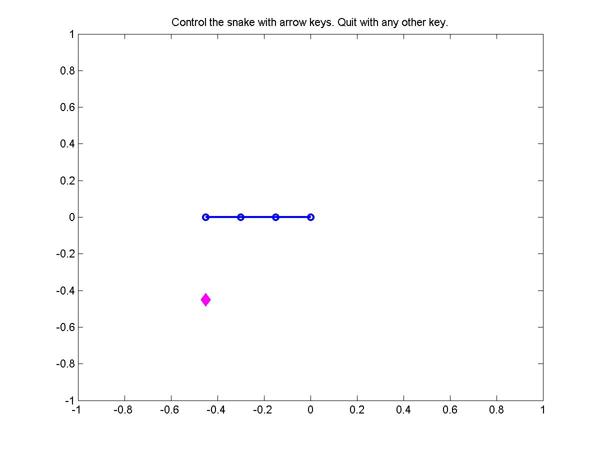
The snake will immediately start to move toward the boundary. If it ever reaches the boundary, or if it ever runs into itself, you lose. You control the snake's movement with the four arrow keys on your keyboard, just like you would have on the VT100, or on your cell phone.
Each time the head of the snake reaches a piece of food, that food disappears, a new piece of food appears at a random spot, the snake grows another node, and begins to move a little faster. Even if you've never seen the game before, I hope you can picture it now.
I really like computer games with simple rules like these.
How do you want them nodes?
Now for the new, mathematical, feature. You can experiment with various kinds of interpolation. Since this is Chebyshev's realm, the default is polynomial interpolation on Chebyshev points. Of course, this behaves very nicely. Then there is a kind of rational interpolation that is unfamiliar to me. But the most fun is polynomial interpolation on equispaced points. You get very wild behavior as the length of the snake grows. Here is just a snapshot.
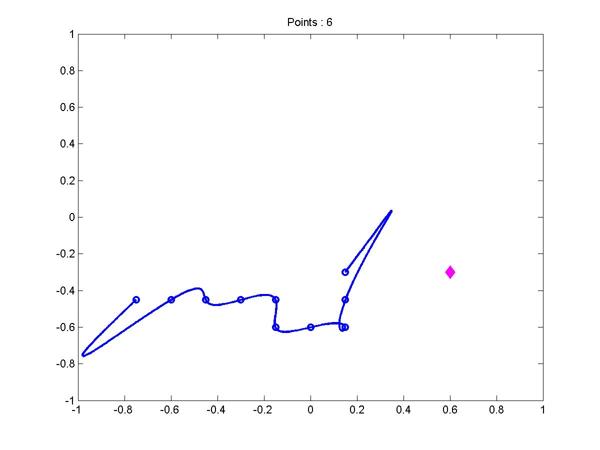
You really have to install Chebfun and see this in action. The dynamic behavior is what caught my attention and prompted me to write this blog. In case you didn't know it already, polynomial interpolation on equispaced points can behave like a snake trying to cross a slippery plot.
- Category:
- Algorithms









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.