Season's Greetings, 2014 help greetings % greetings Seasonal holiday fractal. % greetings(phi) generates a seasonal holiday fractal that depends % upon the parameter phi. The default... 更多内容 >>

An incredible book, published in several editions from 1909 to 1933, by German mathematicians Eugene Jahnke and Fritz Emde, contains definitions and formulas for mathematical functions, hand-calculated tables of function values, and meticulous hand-drawn 2- and 3-dimensional graphs. An English edition was published by Dover in 1945.... 更多内容 >>

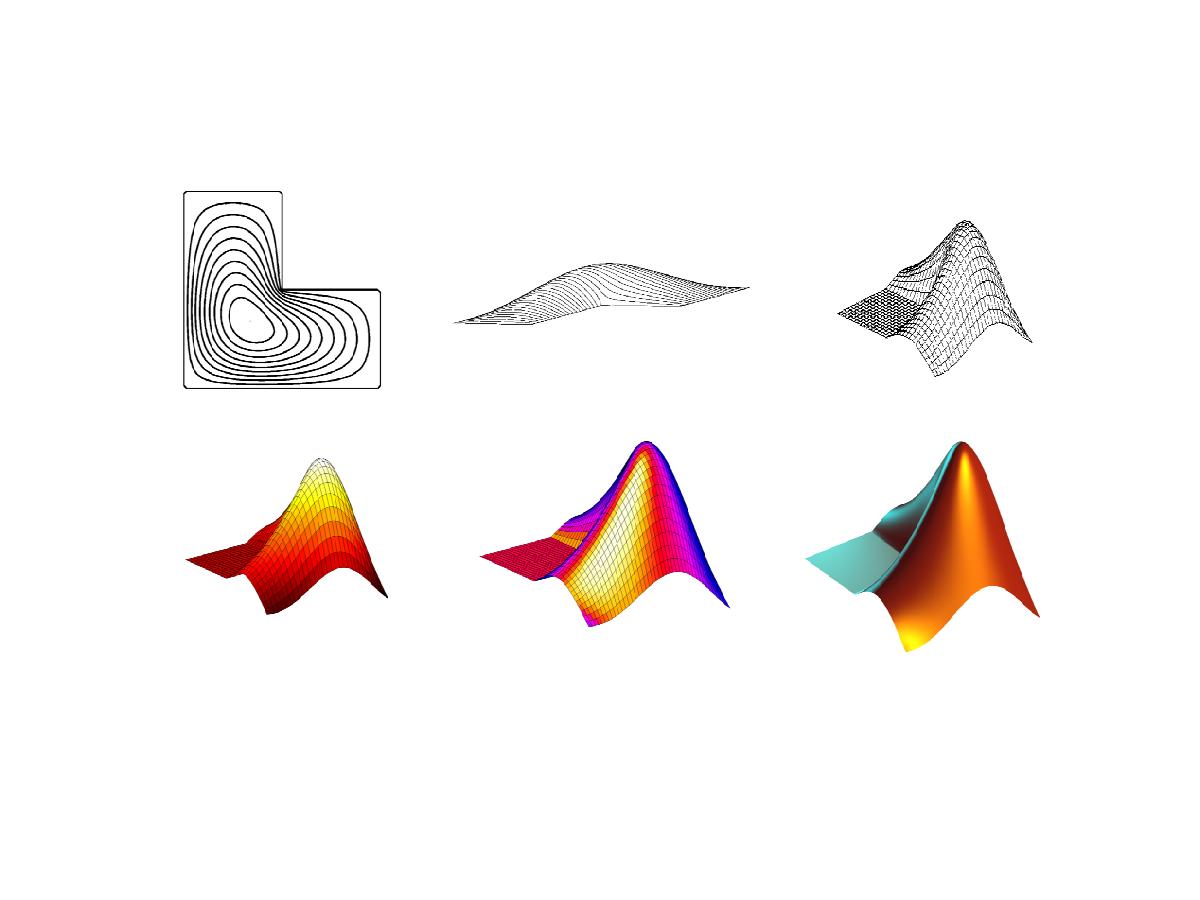
Our plots of the first eigenfunction of the L-shaped membrane have changed several times over the last fifty years.... 更多内容 >>

The Method of Particular Solutions computes a highly accurate approximation to the eigenvalue we have been seeking, and guaranteed bounds on the accuracy. It also provides flexibility involving the boundary conditions that leads to the MathWorks logo. ... 更多内容 >>

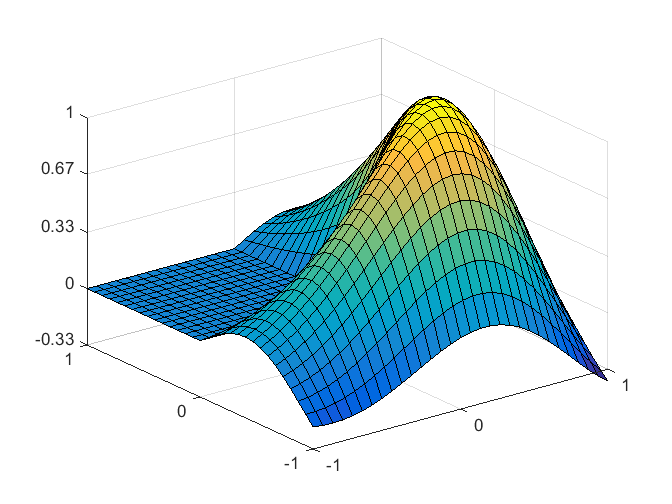
The Partial Differential Equation Toolbox contains tools for the analysis of PDEs in two space dimensions and time. It is perhaps not surprising that one of the primary examples involves the L-shaped membrane.... 更多内容 >>

After reviewing the state of affairs fifty years ago, I use classic finite difference methods, followed by extrapolation, to find the first eigenvalue of the region underlying the MathWorks logo.... 更多内容 >>

MathWorks is the only company in the world whose logo satisfies a partial differential equation. Why is the region for this equation shaped like a capital letter L? ... 更多内容 >>

This is the third in a series of posts on the finite Fourier transform. The Fourier matrix produces an interesting graphic and has a surprising eigenvalue distribution. ... 更多内容 >>

This is the second in a series of three posts about the Finite Fourier Transform. This post is about the fast FFT algorithm itself. A recursive divide and conquer algorithm is implemented in an elegant MATLAB function named ffttx.... 更多内容 >>

We all use Fourier analysis every day without even knowing it. Cell phones, disc drives, DVDs, and JPEGs all involve fast finite Fourier transforms. This post, which describes touch-tone telephone dialing, is the first of three posts about the computation and interpretation of FFTs. The posts are adapted from chapter 8 of my book, Numerical Computing with MATLAB . ... 更多内容 >>