MathWorks Logo, Part Five, Evolution of the Logo
Our plots of the first eigenfunction of the L-shaped membrane have changed several times over the last fifty years.
Contents
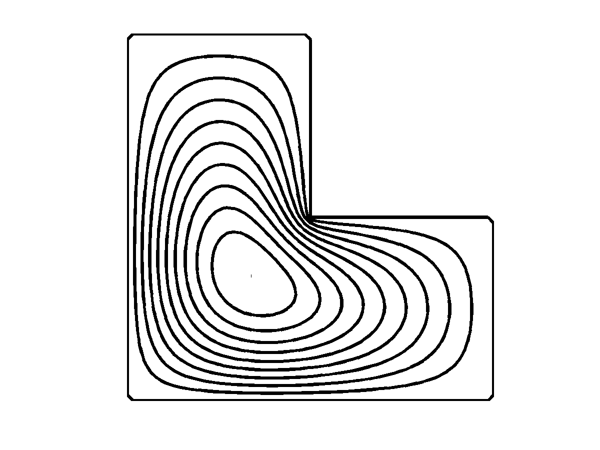
1964, Stanford
Ph.D. thesis. Two dimensional contour plot. Calcomp plotter with ball-point pen drawing on paper mounted on a rotating drum.
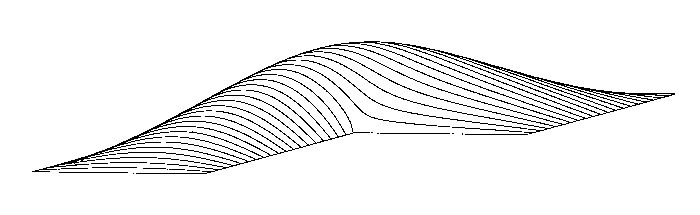
1968, University of Michigan
Calcomp plotter. Math department individual study student project. Original 3d perspective and hidden line algorithms. Unfortunately, I don't remember the student's name.
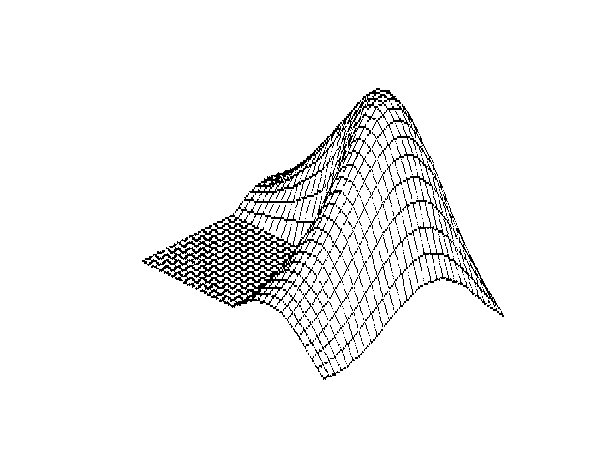
1985, MATLAB 1.0
The first MathWorks documentation and the first surf plot. Apple Macintosh daisy wheel electric typewriter with perhaps 72 dots-per-inch resolution.
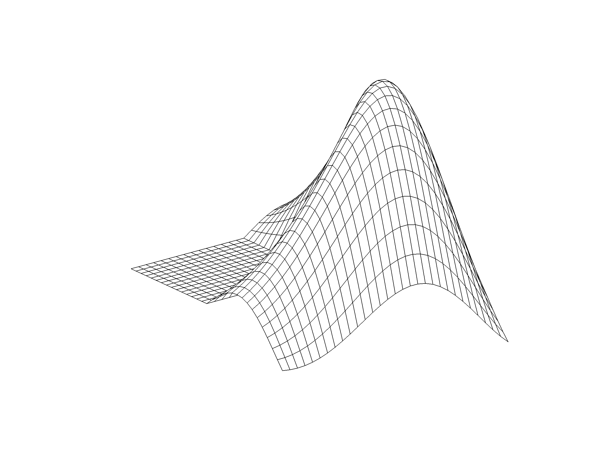
1987, MATLAB 3.5
Laser printer with much better resolution.
1992, MATLAB 4.0
Sun workstation with CRT display and color. Hot colormap, proportional to height.
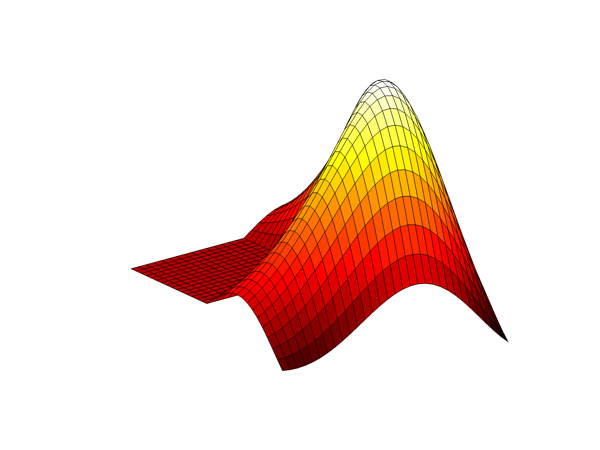
1994, MATLAB 4.2
A hand made lighting model. I have to admit this looks pretty phony today.
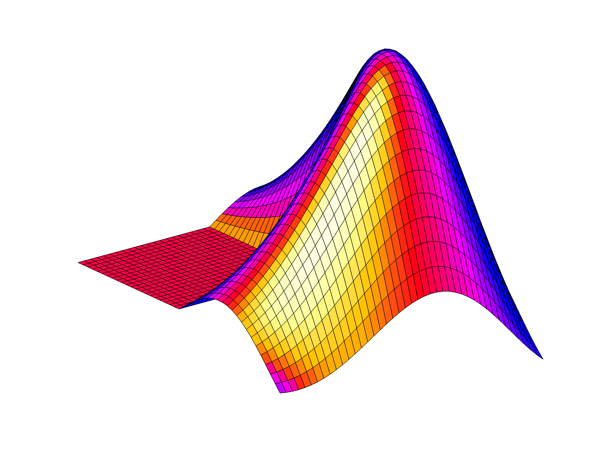
1996, MATLAB 5.0
Good lighting and shading. But at the time this was just a nice graphics demonstration. It was a few more years before it became the official company logo.
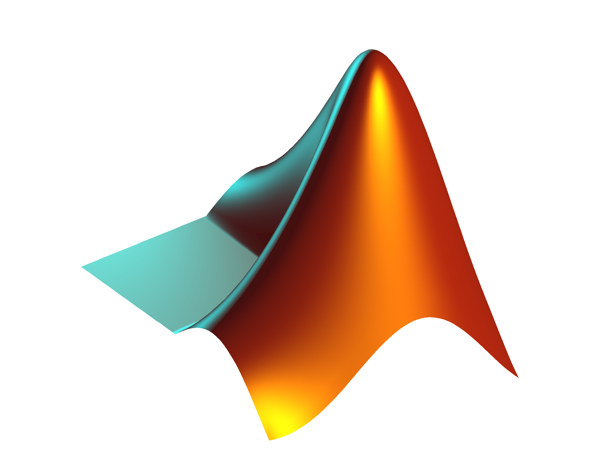
1990, Nantucket Beach
A prototype 3d printer. Pure granular silicon, a few dozen grains per inch. (Thanks to Robin Nelson and David Eells for curating photos.)

More reading
Cleve's Corner, "The Growth of MATLAB and The MathWorks over Two Decades", MathWorks News&Notes, Jan. 2006.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.