Champagne Portraits of Complex Functions
Lots of tiny bubbles.

Contents
Domain
The basic domain is the quadruple unit square,
$$\max{(|x|,|y|)} \le 1, \ z = x+iy $$
Colors
I could use the HSV colormap.
hsv_bubbles(@(z) z)
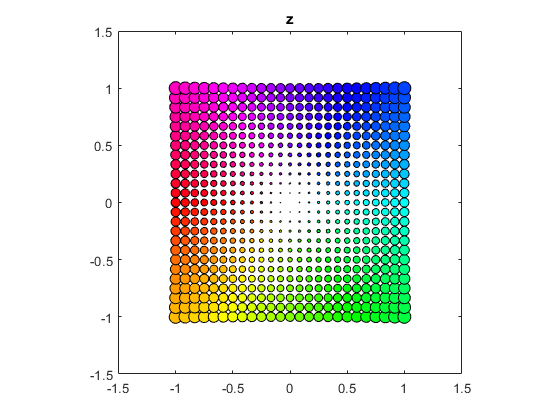
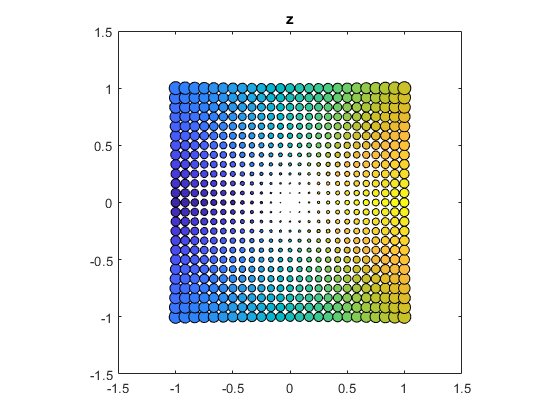
But I prefer "periodic parula", the parula colormap concatenated with its reverse, [parula; flipud(parula)].
bubbles(@(z) z)
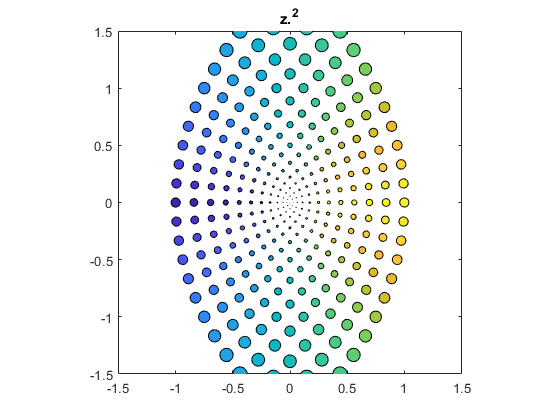
Powers
z^2
bubbles(@(z) z.^2)
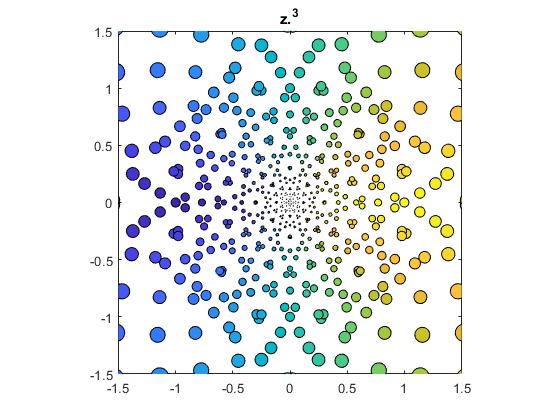
z^3
bubbles(@(z) z.^3)
z^9
bubbles(@(z) z.^9)
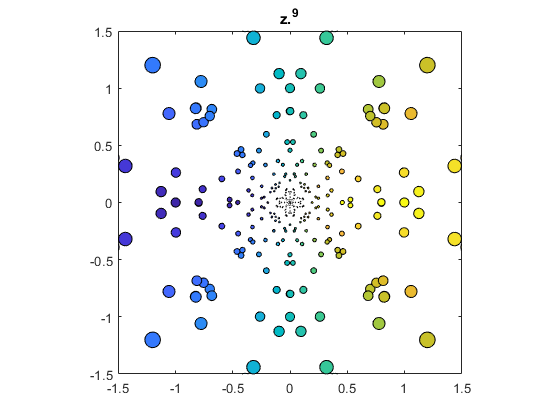
1/z
bubbles(@(z) 1./z)
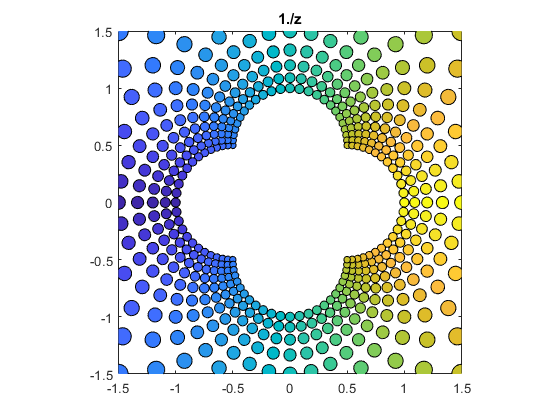
sqrt(z)
A complex number has two square roots. One is in the right half plane.
bubbles(@sqrt)
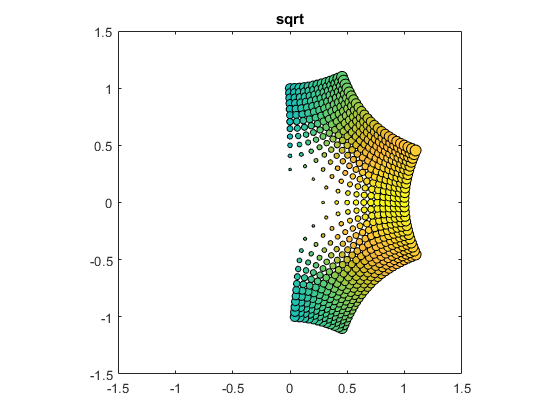
-sqrt(z)
And the other is in the left half plane.
bubbles(@(z) -sqrt(z))
Trig functions
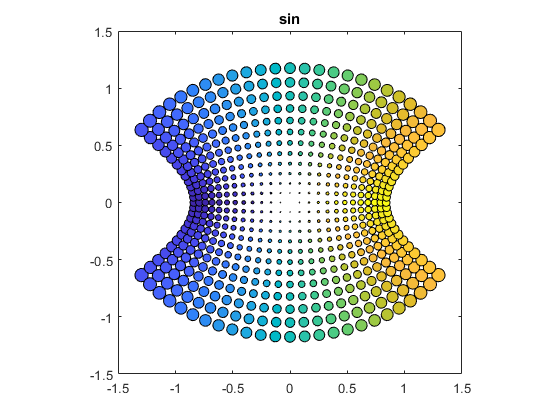
sin(z)
bubbles(@sin)
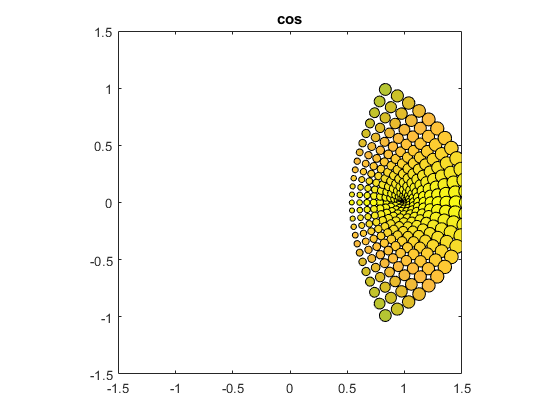
cos(z)
bubbles(@cos)
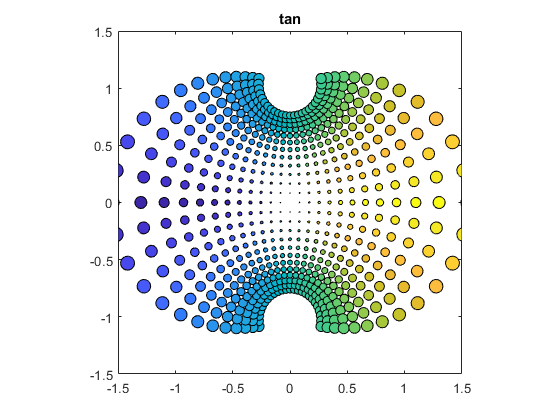
tan(z)
bubbles(@tan)
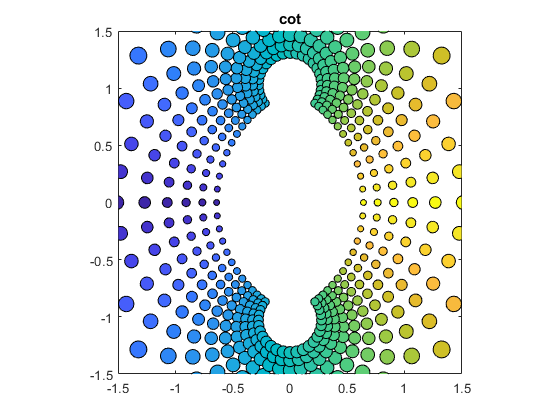
cot(z)
bubbles(@cot)
Exponentials
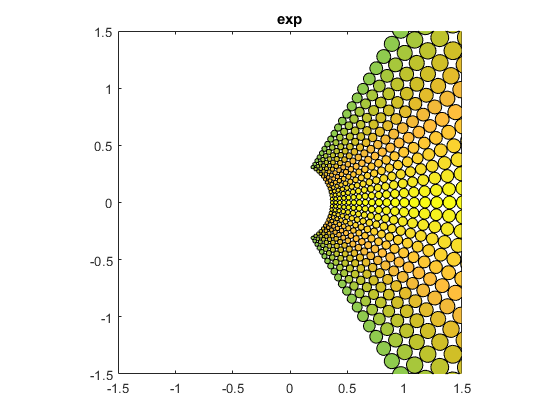
exp(z)
These polar angles are between -1 and +1 radian.
bubbles(@exp)
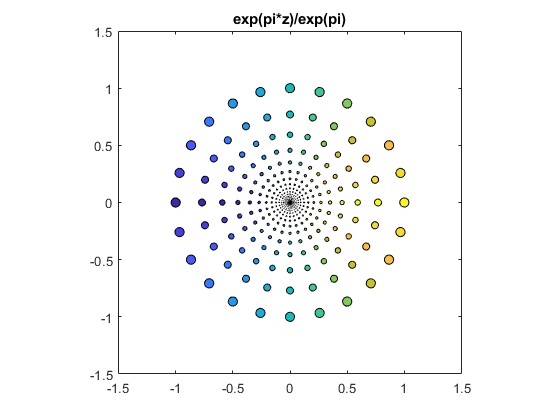
exp(pi*z)/exp(pi)
These fill out the entire complex plane.
bubbles(@(z) exp(pi*z)/exp(pi))
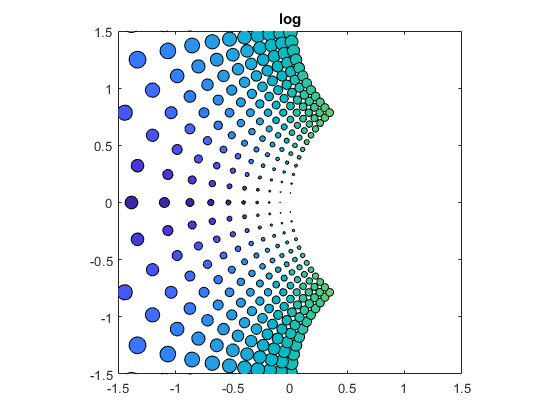
log(z)
bubbles(@log)
Polynomials and rationals
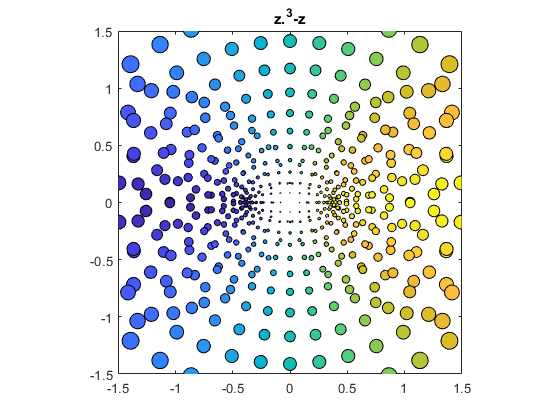
z^3 - z
bubbles(@(z) z.^3-z)
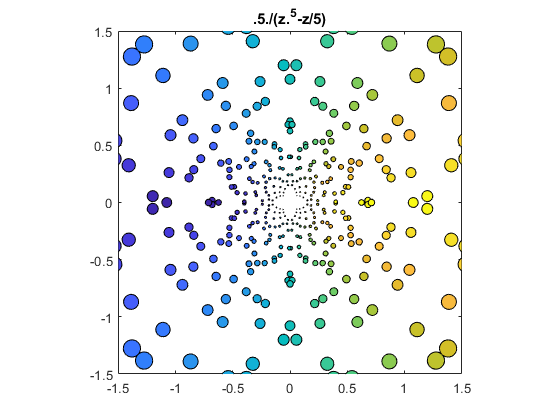
.5/(z^5-z/5)
bubbles(@(z) .5./(z.^5-z/5))
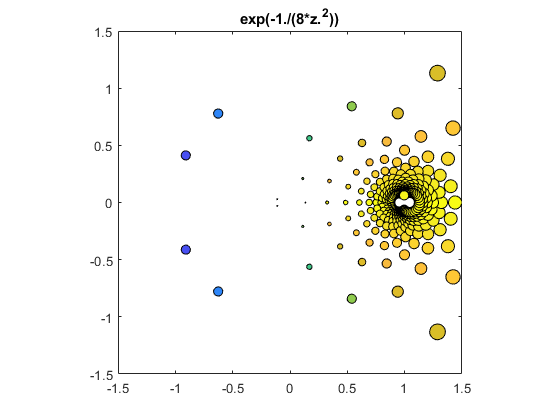
Essential singularity.
exp(-1/(8 z^2)
bubbles(@(z) exp(-1./(8*z.^2)))
Quiz
What is happening in the animation at the top of this post? If you think you know, or even if you just know part of the answer, submit a comment. I'll have some sort of prize for the first, or best, solution.
Code
Also available at https://blogs.mathworks.com/cleve/files/bubbles.m.
type bubbles
function bubbles(F)
% bubbles. Color portrait of complex-valued function F(z),
% ex. bubbles(@sin)
% bubbles(@(z) .5./(z.^5-z/5) )
if nargin < 1
F = @(z)z;
end
axis(1.5*[-1 1 -1 1])
axis square
box on
cla
m = 256;
colormap = [parula(m);flipud(parula(m))];
n = 25;
s = -1:2/(n-1):1;
[x,y] = meshgrid(s);
z = x + y*1i;
circle = exp((0:32)/16*pi*1i)/n;
w = F(z);
r = abs(w);
theta = angle(w)+pi;
scale = 20;
for k = 1:n
for j = 1:n
t = m*theta(k,j)/pi/scale;
idx = ceil(scale*t+realmin);
color = colormap(idx,:);
p = w(k,j) + r(k,j)*circle;
patch(real(p),imag(p),color)
end
end
titleF = char(F);
if (titleF(1) == '@')
titleF(1:4) = [];
end
title(titleF)
snapnow
end
- Category:
- Calculus,
- Color,
- Fun,
- Graphics,
- Special Functions








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.