A Famous Equation, x^2 = 2^x
A recent episode of the popular YouTube channel "blackpenredpen" is about solutions to the famous equation
x^2 = 2^x
You should be able to see two solutions yourself, x = 2 and x = 4, because 2^2 = 2^2 and 4^2 = 2^4.
This post is about a third solution.
Contents
Two graphs
The figure shows the graphs of x^2 and 2^x and their intersections. The narrow silver area is the only region the right half plane where x^2 is greater than 2^x.
We can see there are three intersections -- the two we knew about at x = 2 and x = 4 and a third one at a negative value of x. Blackpen carefully explains how to characterize this negative solution.
black_pen_plot

The negative solution
I was pleased to learn that our Symbolic Math Toolbox can find all three solutions, provided we indicate that we are only interested in real-valued solutions. (The behavior of x^2 = 2^x for complex x is a topic for another day.)
syms x real z = solve(x^2 == 2^x)
z =
2
4
-(2*lambertw(0, log(2)/2))/log(2)
We want to know more about that third solution.
z = z(3)
z = -(2*lambertw(0, log(2)/2))/log(2)
The function lambertw(x) involved in this solution is an old friend, the LambertW function.
Logarithm
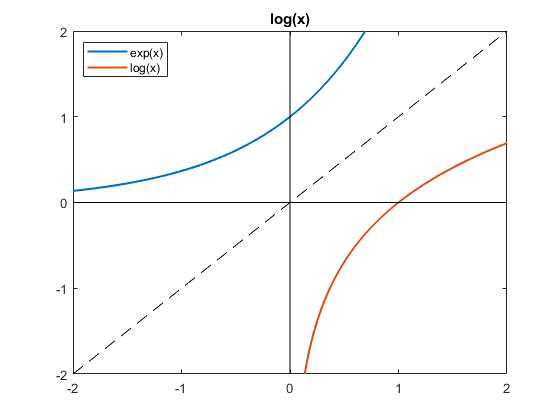
The blue curve in the following figure is a plot of exp(x). It goes to zero for negative x and grows exponentially for positive x. Imagine interchanging the x and y axes by reflecting the blue curve about the diagonal dashed line to produce the orange curve. The orange curve is familiar. It is a plot of the functional inverse of exp(x) which we know as log(x). If y = log(x) then x = exp(y).
log_plot
Current plot released
LambertW
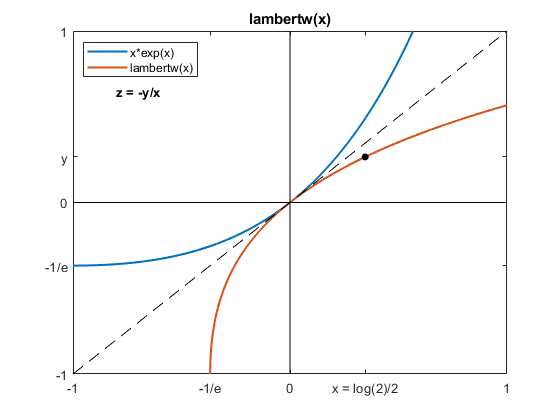
The blue curve in the following figure is now a plot of x*exp(x). Reflecting the blue curve about the diagonal produces the orange curve, a plot of the functional inverse of x*exp(x). This function is not as familiar as log(x). It is lambertw(x). If y = lambertw(x) then x = y*exp(y).
We need to evaluate y = lambertw(x) at x = log(2)/2. This is the black dot. Once we have x and y, the negative solution to our famous equation is simply z = -y/x.
lambertw_plot
Current plot released
Many digits
The Symbolic Math Toolbox variable precision arithmetic, vpa, can produce the numeric value of the negative solution to any number of digits.
z
vpaz = vpa(z,75)
z = -(2*lambertw(0, log(2)/2))/log(2) vpaz = -0.766664695962123093111204422510314848006675346669832058460884376935552795725
Fixed points
Here is your homework. Investigate the iteration:
x = sign(x)*2^(x/2)
Consider three situations:
- Starting values between 0 and 4.
- Starting values greater than 4.
- Starting values less than 0.
Thanks
Thanks to Mark Round for suggesting only real solutions.
Code
The code for the figures is available.
- Category:
- History,
- Numerical Analysis,
- People



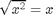





Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.