A Famous Equation, x^2 = 2^x
A recent episode of the popular YouTube channel "blackpenredpen" is about solutions to the famous equation
x^2 = 2^x
You should be able to see two solutions yourself, x = 2 and x = 4, because 2^2 = 2^2 and 4^2 = 2^4.
This post is about a third solution.
Contents
Two graphs
The figure shows the graphs of x^2 and 2^x and their intersections. The narrow silver area is the only region the right half plane where x^2 is greater than 2^x.
We can see there are three intersections -- the two we knew about at x = 2 and x = 4 and a third one at a negative value of x. Blackpen carefully explains how to characterize this negative solution.
black_pen_plot

The negative solution
I was pleased to learn that our Symbolic Math Toolbox can find all three solutions, provided we indicate that we are only interested in real-valued solutions. (The behavior of x^2 = 2^x for complex x is a topic for another day.)
syms x real z = solve(x^2 == 2^x)
z =
2
4
-(2*lambertw(0, log(2)/2))/log(2)
We want to know more about that third solution.
z = z(3)
z = -(2*lambertw(0, log(2)/2))/log(2)
The function lambertw(x) involved in this solution is an old friend, the LambertW function.
Logarithm
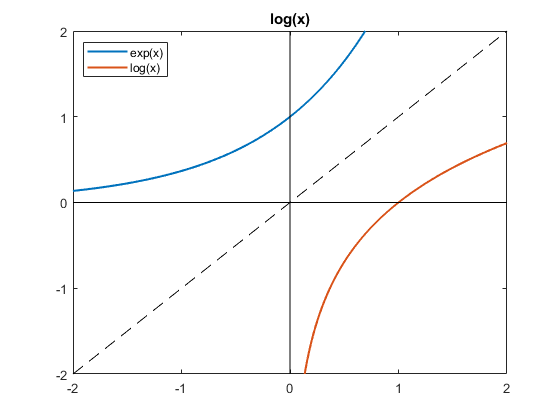
The blue curve in the following figure is a plot of exp(x). It goes to zero for negative x and grows exponentially for positive x. Imagine interchanging the x and y axes by reflecting the blue curve about the diagonal dashed line to produce the orange curve. The orange curve is familiar. It is a plot of the functional inverse of exp(x) which we know as log(x). If y = log(x) then x = exp(y).
log_plot
Current plot released
LambertW
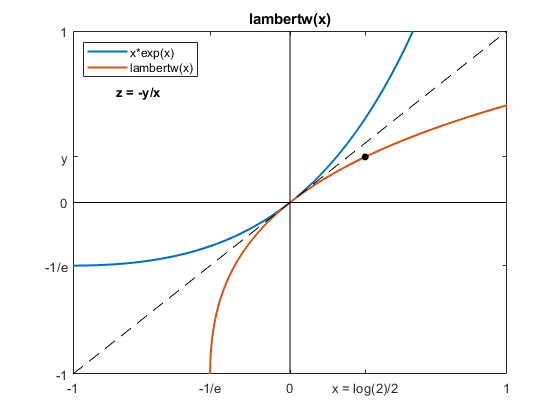
The blue curve in the following figure is now a plot of x*exp(x). Reflecting the blue curve about the diagonal produces the orange curve, a plot of the functional inverse of x*exp(x). This function is not as familiar as log(x). It is lambertw(x). If y = lambertw(x) then x = y*exp(y).
We need to evaluate y = lambertw(x) at x = log(2)/2. This is the black dot. Once we have x and y, the negative solution to our famous equation is simply z = -y/x.
lambertw_plot
Current plot released
Many digits
The Symbolic Math Toolbox variable precision arithmetic, vpa, can produce the numeric value of the negative solution to any number of digits.
z
vpaz = vpa(z,75)
z = -(2*lambertw(0, log(2)/2))/log(2) vpaz = -0.766664695962123093111204422510314848006675346669832058460884376935552795725
Fixed points
Here is your homework. Investigate the iteration:
x = sign(x)*2^(x/2)
Consider three situations:
- Starting values between 0 and 4.
- Starting values greater than 4.
- Starting values less than 0.
Thanks
Thanks to Mark Round for suggesting only real solutions.
Code
The code for the figures is available.
- Category:
- History,
- Numerical Analysis,
- People
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.