Round, With Tie Breakers, Round Three
I recently published Round, With Ties to Even and followed that with Round Two. Then, in an email, Andy Bartlett pointed out that my new round function fails for some large values of x between flintmax/2 and flintmax.
Contents
flintmax/2
The quantity f = flintmax/2 is equal to 2^52, which is 1/eps. The help entry for format bank says it is a fixed format for dollars and cents. That's true, but I also like to use it for displaying large flints.
format bank
f = flintmax/2
f = 4503599627370496.00
The numbers in the interval [f flintmax] are the largest flints. They are all integers. The spacing between them is one.
eps(f)
ans =
1.00
All floating point numbers larger than flintmax are integers, but the spacing between is larger than one, so they cannot be used for integer arithmetic.
Rounding
The idea behind all versions of round is the following. Suppose abs(x) is between two integers, y-1 and y. Then
a = abs(x) + 0.5;
is between y-0.5 and y+0.5. And
r = floor(a);
is equal to either y-1 or y, whichever is closer to abs(x).
That idea works for almost all x. However, if x is between f and flintmax, the quantity x + 0.5 is not a floating point number and must itself be rounded to the nearest even by the addition hardware. If y is odd, the resulting a will be y+1, which is too large.
So, I must compute a by
a = abs(x) + (0.5 - eps/4);
The quantity (0.5 - eps/4) is the next smaller floating point number less that 0.5.
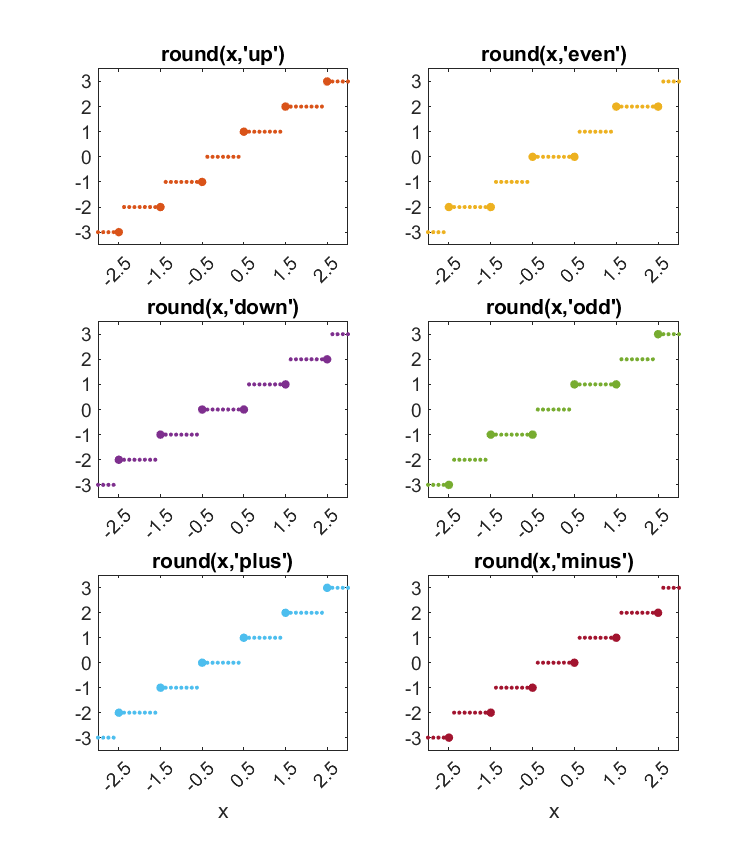
round
This is the resulting proposal for the enhancement request on round. It is available here. Only the line computing a has changed from Round Two.
type Round.m
function r = round(varargin)
% r = round(x) scales and rounds the elements of x to the nearest integers.
% Default: ties, elements halfway between integers, are rounded away from zero.
%
% r = round(x,'even') ties round to even integers.
% r = round(x,'odd') ties round to odd integers.
% r = round(x,'up') ties round away from zero (same as default).
% r = round(x,'down') ties round towards zero.
% r = round(x,'plus') ties round to the right on the number line.
% r = round(x,'minus') ties round to the left on the number line.
%
% r = round(x,n), n >= 0, round(10^n*x)/10^n, round(12.3456,2) = 12.3500
% r = round(x,-n), n > 0, 10^n*round(x/10^n), round(1234.56,-2) = 1200.
% r = round(x,n,'significant'), round(.001234,2,'significant') = .0012
% r = round(x,n,'decimals) same as round(x,n).
%
% r = round(x,...), ties, n, 'significant' and 'decimals' can be in any order.
%
% Use Round(...) with capital R to distinguish from built-in round(...).
[x,n,ties] = parse_input(varargin{:});
x = prescale(x,n);
a = abs(x) + (0.5-eps/4);
r = floor(a);
switch ties
case 'even'
m = (r == a) & (mod(r,2) == 1);
case 'odd'
m = (r == a) & (mod(r,2) == 0);
case 'down'
m = (r == a);
case 'up'
m = [];
case 'plus'
m = (x < 0) & (r == a);
case 'minus'
m = (x > 0) & (r == a);
otherwise
error(['''' ties ''' not recognized.'])
end
r(m) = r(m) - 1;
r = sign(x).*r;
r = postscale(r,n);
% ----------------------------------------------
function [x,n,ties] = parse_input(varargin)
x = varargin{1};
n = zeros(size(x));
ties = 'up';
for k = 2:nargin
if isnumeric(varargin{k})
n(:) = varargin{k};
elseif strcmp(varargin{k},'significant')
n(:) = n(:) - ceil(log10(abs(x(:))));
elseif strcmp(varargin{k},'decimals')
% ignore
else
ties = varargin{k};
end
end
end
function x = prescale(x,n)
if any(n ~= 0)
k = n > 0;
x(k) = 10.^n(k).*x(k);
k = n < 0;
x(k) = x(k)./10.^(-n(k));
end
end
function r = postscale(r,n)
if any(n ~= 0)
k = n > 0;
r(k) = r(k)./10.^n(k);
k = n < 0;
r(k) = 10.^(-n(k)).*r(k);
end
end
end
test
The vector x = f:flintmax would have 2^52+1 elements. That's too many. The first four and the last four is enough.
format hex x = [f+(0:3); 2*f-(3:-1:0)] r = Round(x) up = Round(x,'up') down = Round(x,'down') even = Round(x,'even') odd = Round(x,'odd') plus = Round(x,'plus') minus = Round(x,'minus')
x = 4330000000000000 4330000000000001 4330000000000002 4330000000000003 433ffffffffffffd 433ffffffffffffe 433fffffffffffff 4340000000000000 r = 4330000000000000 4330000000000001 4330000000000002 4330000000000003 433ffffffffffffd 433ffffffffffffe 433fffffffffffff 4340000000000000 up = 4330000000000000 4330000000000001 4330000000000002 4330000000000003 433ffffffffffffd 433ffffffffffffe 433fffffffffffff 4340000000000000 down = 432ffffffffffffe 4330000000000000 4330000000000001 4330000000000002 433ffffffffffffc 433ffffffffffffd 433ffffffffffffe 433fffffffffffff even = 4330000000000000 4330000000000000 4330000000000002 4330000000000002 433ffffffffffffc 433ffffffffffffe 433ffffffffffffe 4340000000000000 odd = 432ffffffffffffe 4330000000000001 4330000000000001 4330000000000003 433ffffffffffffd 433ffffffffffffd 433fffffffffffff 433fffffffffffff plus = 4330000000000000 4330000000000001 4330000000000002 4330000000000003 433ffffffffffffd 433ffffffffffffe 433fffffffffffff 4340000000000000 minus = 432ffffffffffffe 4330000000000000 4330000000000001 4330000000000002 433ffffffffffffc 433ffffffffffffd 433ffffffffffffe 433fffffffffffff
- Category:
- Numerical Analysis,
- Precision,
- Programming






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.