Estimating pi Using Buffon’s Method

I recently attended the ICIAM meeting in Valencia, Spain which meant I got to hang out with my pals Carlos Sanchis and Lucas Garcia :-)! Carlos showed me a problem he was working with Professor Fernando Giménez from UPV regarding an app for estimating $\pi$ using Buffon's method. Here's the problem statement from Wikipedia:

Suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle onto the floor. What is the probability that the needle will lie across a line between two strips?

Interesting that the original intention had nothing to do with computing $\pi$ ! There's some fun, powerful, yet fairly easy code to demonstrate the algorithm.

Contents

Set Up Parameters

How many line segments?

N = 1000;

Length of each line?

L = 0.20;

We want the beginning points of the lines to lie between L and 1-L so we don't go outside the unit square.

xb = L + rand(1,N)*(1-2*L);
yb = L + rand(1,N)*(1-2*L);
angs = rand(1,N)*360;
xe = xb + L*cosd(angs);
ye = yb + L*sind(angs);

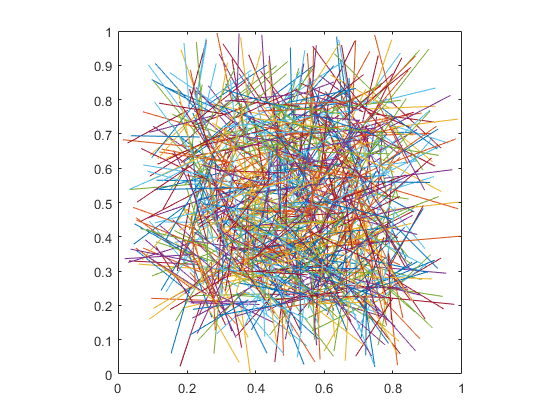
Visualize the Lines

ax = axes;
plot(ax,[xb;xe],[yb;ye])
axis square

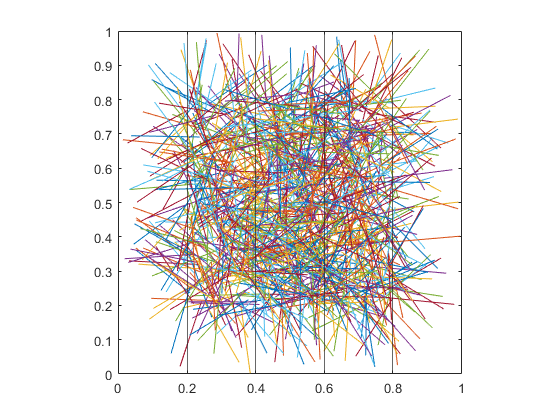
Show the Vertical Grid Lines Defined by L Spacing

hold on
glines = 0:L:1;
for i = 1:length(glines)
   xline(ax, glines(i));
end

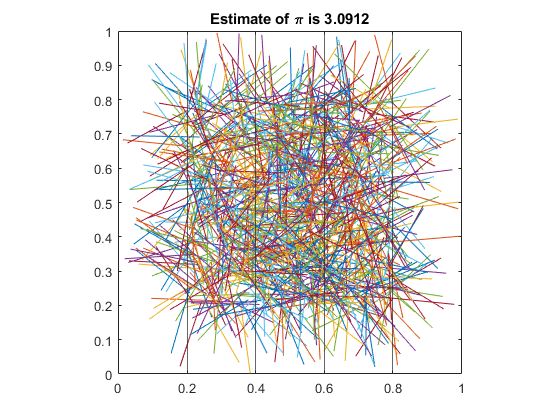
Count the Segments Intersecting the Grid

n = sum(floor(xb/L) ~= floor(xe/L));
piEstimate = 2 * N / n

piEstimate =
    3.1153

Annotate Final Plot

title("Estimate of \pi is " + piEstimate)

What Happens as L and N change?

This could be a great exercise for the classroom - seeing how the estimates depend on how many line segments and the spacing of the grid. Not to mention running a bunch of times with different random numbers each time. What simple estimation problems do you like to use? Let me know here.

Get the MATLAB code

Published with MATLAB® R2019a