Estimating pi Using Buffon’s Method
I recently attended the ICIAM meeting in Valencia, Spain which meant I got to hang out with my pals Carlos Sanchis and Lucas Garcia :-)! Carlos showed me a problem he was working with Professor Fernando Giménez from UPV regarding an app for estimating $\pi$ using Buffon's method. Here's the problem statement from Wikipedia:
Suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle onto the floor. What is the probability that the needle will lie across a line between two strips?
Interesting that the original intention had nothing to do with computing $\pi$ ! There's some fun, powerful, yet fairly easy code to demonstrate the algorithm.
Contents
Set Up Parameters
How many line segments?
N = 1000;
Length of each line?
L = 0.20;
We want the beginning points of the lines to lie between L and 1-L so we don't go outside the unit square.
xb = L + rand(1,N)*(1-2*L); yb = L + rand(1,N)*(1-2*L); angs = rand(1,N)*360; xe = xb + L*cosd(angs); ye = yb + L*sind(angs);
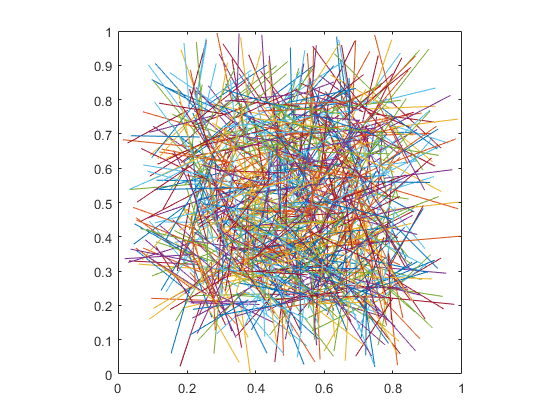
Visualize the Lines
ax = axes;
plot(ax,[xb;xe],[yb;ye])
axis square
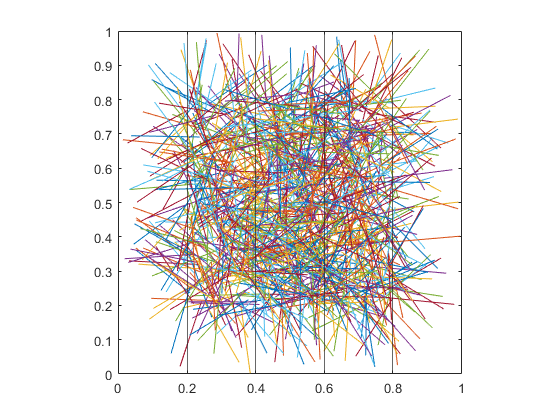
Show the Vertical Grid Lines Defined by L Spacing
hold on glines = 0:L:1; for i = 1:length(glines) xline(ax, glines(i)); end
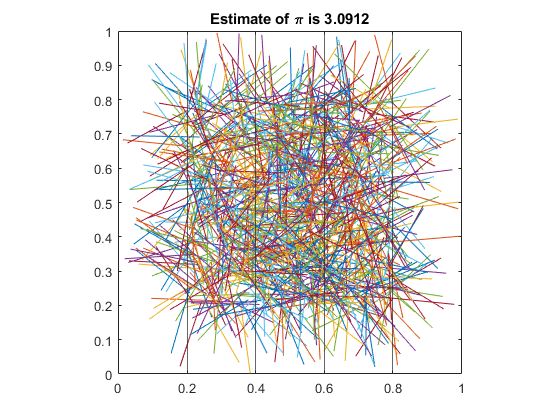
Count the Segments Intersecting the Grid
n = sum(floor(xb/L) ~= floor(xe/L)); piEstimate = 2 * N / n
piEstimate =
3.1153
Annotate Final Plot
title("Estimate of \pi is " + piEstimate)
What Happens as L and N change?
This could be a great exercise for the classroom - seeing how the estimates depend on how many line segments and the spacing of the grid. Not to mention running a bunch of times with different random numbers each time. What simple estimation problems do you like to use? Let me know here.
- Category:
- Fun









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.