Estimating pi Using Buffon’s Method
I recently attended the ICIAM meeting in Valencia, Spain which meant I got to hang out with my pals Carlos Sanchis and Lucas Garcia :-)! Carlos showed me a problem he was working with Professor Fernando Giménez from UPV regarding an app for estimating $\pi$ using Buffon's method. Here's the problem statement from Wikipedia:
Suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle onto the floor. What is the probability that the needle will lie across a line between two strips?
Interesting that the original intention had nothing to do with computing $\pi$ ! There's some fun, powerful, yet fairly easy code to demonstrate the algorithm.
Contents
Set Up Parameters
How many line segments?
N = 1000;
Length of each line?
L = 0.20;
We want the beginning points of the lines to lie between L and 1-L so we don't go outside the unit square.
xb = L + rand(1,N)*(1-2*L); yb = L + rand(1,N)*(1-2*L); angs = rand(1,N)*360; xe = xb + L*cosd(angs); ye = yb + L*sind(angs);
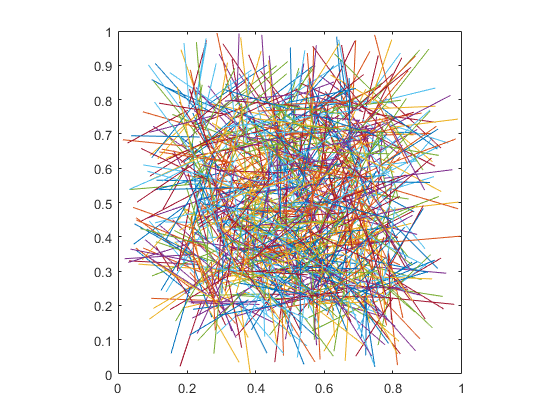
Visualize the Lines
ax = axes;
plot(ax,[xb;xe],[yb;ye])
axis square
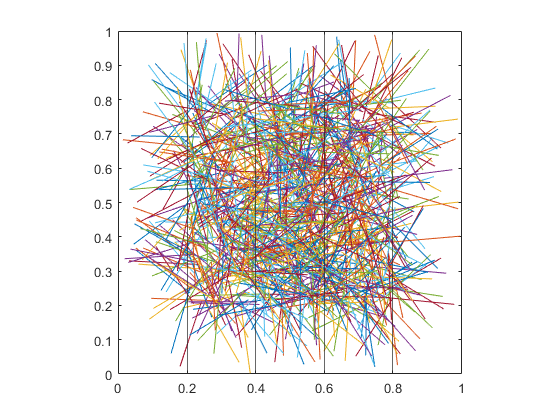
Show the Vertical Grid Lines Defined by L Spacing
hold on glines = 0:L:1; for i = 1:length(glines) xline(ax, glines(i)); end
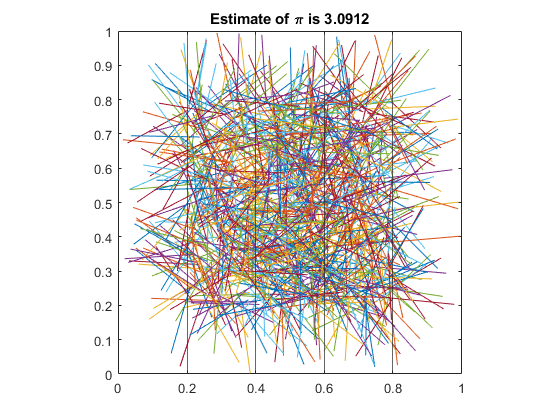
Count the Segments Intersecting the Grid
n = sum(floor(xb/L) ~= floor(xe/L)); piEstimate = 2 * N / n
piEstimate =
3.1153
Annotate Final Plot
title("Estimate of \pi is " + piEstimate)
What Happens as L and N change?
This could be a great exercise for the classroom - seeing how the estimates depend on how many line segments and the spacing of the grid. Not to mention running a bunch of times with different random numbers each time. What simple estimation problems do you like to use? Let me know here.
- Category:
- Fun
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.