Last week I wrote about a possible modification to poly2mask that would estimate how much of each pixel is contained within a polygon. The idea was to use a regular 5-by-5 subgrid and count how many of the 25 subpixels are contained within the polygon. It would look something like this:
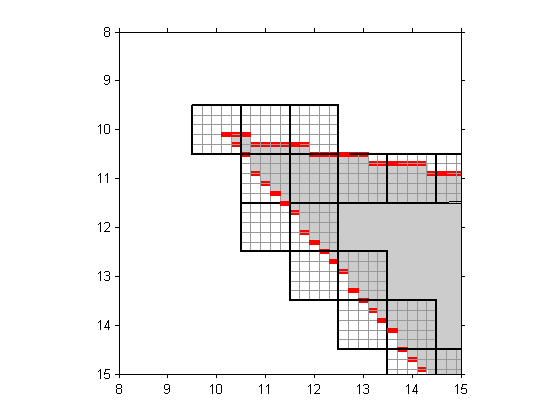
One of our graphics developers, Mike, sent me a note a couple of days later. He pointed out that using a regular N-by-N subsampling of the pixel doesn't do very well for polygon edges that are nearly vertical or horizontal. With a vertical or horizontal edge, your estimate of the pixel coverage is good only to within about 1/N instead of 1/N^2. As a possible alternative, Mike pointed me to something called a Costas array .
A Costas array is a permutation matrix. A permutation matrix contains 0s and 1s such that each row and each column contains only a single 1. The identity matrix is a trivial example:
eye(3)
ans =
1 0 0
0 1 0
0 0 1
In addition to being a permutation matrix, a Costas array has the property that no pair of 1-valued elements has the same vector difference as any other pair. The 3-by-3 identity matrix above does not have this property. The vector difference between the (1,1) element and the (2,2) element is (1,1). This is the same as the vector difference between the (2,2) and (3,3) elements. Here's a visualization of a 10-by-10 Costas array:
v = [2 4 8 5 10 9 7 3 6 1]; n = 10; plot(1:n, v, 'LineStyle', 'none', 'Marker', 'o', ... 'MarkerEdgeColor', 'b', 'MarkerFaceColor', 'b') axis equal grid on set(gca, ... 'XTick', 0.5:(n+0.5), ... 'YTick', 0.5:(n+0.5), ... 'XLim', [0.5 (n+0.5)], ... 'YLim', [0.5 (n+0.5)], ... 'XTickLabel', '', ... 'YTickLabel', '', ... 'GridLineStyle', '-')
And here's a 29-by-29 example:
v = [3 21 23 22 8 15 26 6 16 11 28 5 2 18 10 14 12 13 27 20 9 29 19 ... 24 7 1 4 17 25]; n = 29; plot(1:n, v, 'LineStyle', 'none', 'Marker', 'o', ... 'MarkerEdgeColor', 'b', 'MarkerFaceColor', 'b') axis equal grid on set(gca, ... 'XTick', 0.5:(n+0.5), ... 'YTick', 0.5:(n+0.5), ... 'XLim', [0.5 (n+0.5)], ... 'YLim', [0.5 (n+0.5)], ... 'XTickLabel', '', ... 'YTickLabel', '', ... 'GridLineStyle', '-')
Using the same basic procedure I described last time, you could count how many of the 29 dots lie within the polygon and then divide by 29 to get your coverage estimate.
There are many possible variations on this technique, and Mike assures me that it is an active area of research in computer graphics.
Costas arrays were originally described in the context of waveform detection. See J. Costas, "A Study of a Class of Detection Waveforms Having Nearly Ideal Range-Doppler Ambiguity Properties," Proceedings of the IEEE, vol. 72, no. 8, August 1984. If you want to learn more, start at www.costasarrays.org.
Get
the MATLAB code
Published with MATLAB® 7.3
Hi, Steve:
Interesting your blog post about poly2mask and roipoly. But I have a doubt on them: is that possible to copy a region of interest from an image and put this ROI in a new image with only this ROI?
Thanks in advance,
JanKees
JanKees - Use logical indexing to copy the pixel values inside a region of interest from one image to another. You might do something like this:
Hi, Steve:
I’m Interesting your blog about costas arrays. can you give a matlab example of generating Welch-constructed or Golomb-constructed costas arrays?
Hi, Steve: I meet a problem and need your help. I am now doing some research on image information extraction. My question is: I know the corner points on one object, I take the picture of the object, and get the image. Using corner points detector, I can find the corresponding images of these corners. But these images are different from the corners images calculated by using the perspective camera model. How can I get the actual corner image points from the image of the object? (I mean the images of the corners calculated by using the perspective camera model).
Zhen - Camera calibration can be a fairly involved operation, and I don’t know that much about it. I suggest searching for information on “camera calibration.” You should be able to find some implementations in MATLAB, including contributions on the MATLAB Central File Exchange.
Jianquan - I wish I could give you a MATLAB example showing you how to generate a Costas array. But when I was doing research for this blog posting, I didn’t find any MATLAB implementations. Although the topic interests me somewhat, it is off the main topic for this blog, so I don’t plan to spend more time on it. I suggest you visit the link I mentioned (www.costasarrays.org) and look up the papers mentioned there for generating algorithms.
Are Costas arrays optimal for this task (antialiasing) in any sense? Is there any literature on the issue? Thanks.
A - I posed your question to graphics developer Mike, who first told me about Costas arrays. He pointed out that the success of an antialiasing method depends on properties of human visual perception, and so mathematical measures of optimality tend to be not very helpful. In his experience, “sampling patterns have often been chosen in pretty ad hoc ways with little concern for the underlying math.” He suggests looking through Solomon Golomb’s papers for information about the mathematical properties of Costas arrays.
Hello, Steve. I’m looking for an easy way to calculate for a given polygon (type uint8 or double) for each pixel not only if it lies in the polygon, but also the coverage, e.g. something like 0.65 of a pixel is covered by the polygon.
Do you know any matlab algorithms, which might help me.
Thanks in Advance,
Simon
Simon—This post and my February 6th post are about a possible method for computing partial pixel coverage. I asked whether anyone was interested. We would like to hear about your use case. Can you describe the scenario in which you’d like to be able to compute this information? What kind of data, where did it come from, how will partial pixel coverage be used? What trouble does it cause if this algorithm is not available?
Hello, Steve.
Right now we are using the matlab function poly2mask to intersect different drainage areas/patches with image pixels of a rain radar (e.g. 200×200 pixel, 1km² rastersize).
Those patches are available as dxf-polygones, the radar information is represented by greyscale images.
Since every patch is covered by only 20-30 radar pixels we would like to calculate the exact amount of rainfall for a patch. Nevertheless we are achieving quite good results with the existing poly2mask method.
Simon—Thanks for the information.
hai steve,
congrats for maintainig a good blog.steve i want few costas sequences for N=8 and 10. could you help me out in this regard
Varma—This post contains about everything I know about Costas arrays. I suggest that you follow the link at the end of the post to find some papers and examples.
lots of information here:
www.costasarrays.org
Scott—Thanks. That link is already at the bottom of my post.