Filling holes in images
Didja know? You can fill holes, or pits, in grayscale images by using the Image Processing Toolbox function imfill.
The other day I was rereading the Tarboton paper on upslope area, trying to decide what to do next in my series on that topic. I noticed that the author described filling in "pits" in digital elevation models (DEMs) as a common preprocessing step. He outlined a method based on pixel flow directions, but didn't give details. I realized that this preprocessing step is very easy to do using the Image Processing Toolbox, but that many users might not know about this capability.
Let me first define a little more precisely what I mean by "pit" or "hole," and then I'll show you how to fill it in. It's a little easier to show in one dimension, so let's start there.
Here's a one-dimensional function:
t = linspace(0, 3*pi, 100); y = t/2 + sin(t); plot(t,y)
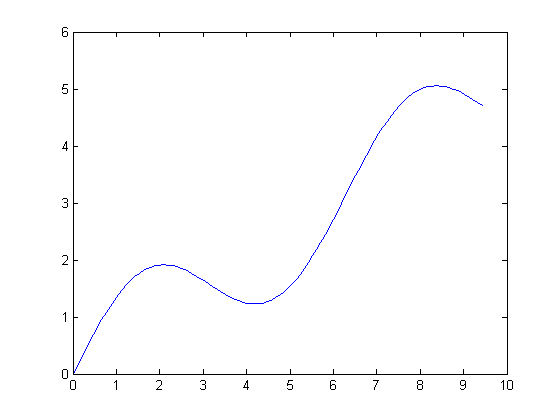
The plot above has a local minimum in its interior. This is a hole, or pit. If we are careful to define our connectivity appropriately for one dimension, we can use imfill with the 'holes' option to fill in the hole.
% Define a one-dimensional connectivity in the horizontal direction. conn = [0 0 0; 1 1 1; 0 0 0]; y2 = imfill(y, conn, 'holes'); plot(t,y2)
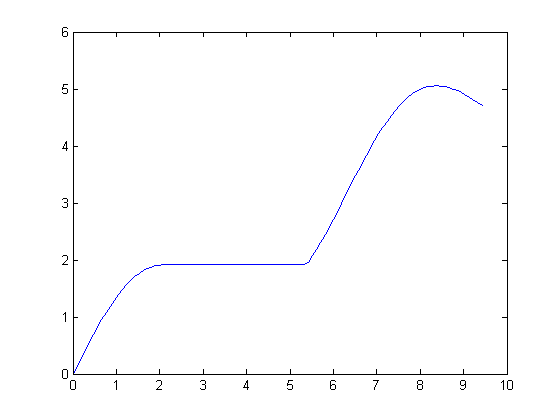
The filled curve has this key property: From any interior point, you can now travel to a boundary minimum without ever going uphill. Here's what it looks for an image:
I = imread('tire.tif'); I2 = imfill(I,'holes'); % the default connectivity is fine subplot(1,2,1) imshow(I) title('Original image') subplot(1,2,2) imshow(I2) title('Filled image')
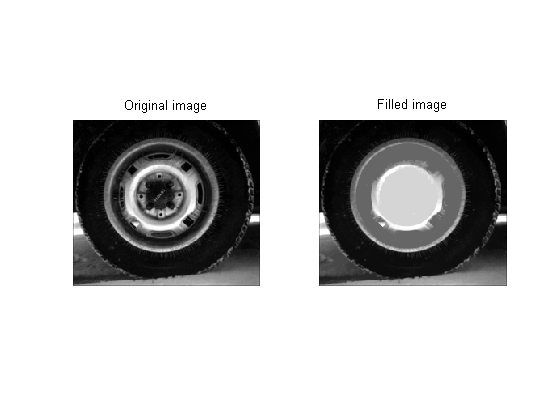
The hole-filling algorithm in imfill is based on morphological reconstruction (imreconstruct). If you are interested in the theoretical details, see section 6.3.7 of Morphological Image Analysis: Principles and Applications, 2nd ed., Springer, by P. Soille.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.