Fourier transforms, vertical lines, and horizontal lines
A reader asked in a blog comment recently why a vertical line (or edge) shows up in the Fourier transform of an image as a horizontal line. I thought I would try to explain this using the simplest example I could think of.
I'll start with an image that is a constant black except for a single vertical line through the middle of it.
x = zeros(200, 200); x(:, 100) = 1; imshow(x)

Next I'll compute and display the log magnitude of the 2-D Fourier transform.
X = fft2(x); imshow(fftshift(log(abs(X) + 1)), [])

There's the question in black and white, so to speak: Why is there a horizontal line in the 2-D Fourier transform?
Although I'm going to avoid equations and other complicated mumbo-jumbo in my answer, I do have to explain a couple of things about 1-D and 2-D Fourier transforms.
First, the magnitude of the 1-D Fourier transform an "impulse sequence" is a constant. An "impulse sequence" is a sequence that is nonzero only at one place, like this one:
x1 = [0 0 1 0 0]
x1 =
0 0 1 0 0
The magnitude of the 1-D Fourier transform of x is constant:
abs(fft(x1))
ans =
1.0000 1.0000 1.0000 1.0000 1.0000
Second, the magnitude of the 1-D Fourier transform of a constant sequence is an impulse. That is, the Fourier transform is nonzero only at one place.
x2 = [1 1 1 1 1]
x2 =
1 1 1 1 1
abs(fft(x2))
ans =
5 0 0 0 0
Finally, computing the 2-D Fourier transform is mathematically equivalent to computing the 1-D Fourier transform of all the rows and then computing the 1-D Fourier transforms of all the columns of the result. The order (row-first or column-first) doesn't actually matter.
Now let's go back to x, our 200-by-200 matrix with a vertical line down the middle of it. Each row of x is an impulse sequence:
plot(x(50,:))

So if we compute the Fourier transform of all the rows, they'll all be constant (in magnitude):
X_rows = fft(x, [], 2); plot(abs(X_rows(50, :))) ylim([0 2])

The next step in computing the 2-D Fourier transform is to compute the 1-D Fourier transforms of the columns of X_rows. But those columns are constant. Here's the 100th column of X_rows:
plot(abs(X_rows(:, 100))) ylim([0 2])

As I said above, the Fourier transform of a constant sequence is an impulse. If you stack up all the resulting columns containing impulse sequences, the result looks like a horizontal line.
X = fft(X_rows, [], 1); imshow(fftshift(log(abs(X) + 1)), [])

That's a step-by-step computational explanation. Let me leave you with more of a conceptual (that is, hand-wavy) explanation. Let's look at the input image and the 2-D Fourier transform side by side.
subplot(1,2,1) imshow(x) title('x') subplot(1,2,2) imshow(fftshift(log(abs(X) + 1)), []) title('Log magnitude of fft2(x)')

You can think in terms of horizontal and vertical cross-sections. Each horizontal cross-section of x is an impulse sequence. The Fourier transform of an impulse sequence is constant, so horizontal cross-sections of the Fourier transform are constant.
Similarly, each vertical cross-section of x is a constant sequence. The Fourier transform of a constant sequence is an impulse sequence, so the vertical cross-sections of the Fourier transform are impulses. The impulses all line up each other, resulting in the appearance of a horizontal line.
Do these explanations work for you? Do you know of another way to think about it that makes a better explanation? Post your thoughts as comments below.
- Category:
- Fourier transforms
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building


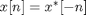

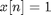



Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.