Can You Find Love through Text Analytics?

Contents
Love Experiment
I read a very intriguing New York Times article To Fall in Love With Anyone, Do This. It was about an experiment that went like this:
“Two heterosexual strangers sat face to face in a lab and answered a series of 36 increasingly personal questions. Then they stared silently into each other’s eyes for four minutes. Six months later, they were married.”
I wanted to see if someone could try it. Luckily, a friend of mine in Japan was keen to give it a try, but there was one minor issue: she couldn’t find any male counterpart who was willing to join her in this experiment.
This is a big issue in Japan where the birthrate went negative. There is even a new word, Konkatsu, for the intensive effort required to get married. Before we can do this experiment, we need to solve this problem first. A lot of people turn to online dating for that, but that is not so easy, either. Do you need some evidence?
Latent Semantic Analysis with MATLAB
In an online dating world you need to comb through a mind-numbing volume of profiles just to get started. Then came the idea: why not use MATLAB to mine online profiles to find your love?
We need data to analyze. I don’t have access to real online dating profiles, but luckily I found Online Dating Ipsum by Lauren Hallden that randomly generates fictitious ones. I used Latent Semantic Analysis (LSA) to cluster online profiles based on the words they contain. I cooked up a MATLAB class myLSA.m to implement Latent Semantic Analysis methods. Let’s initialize it into an object called LSA, and load the dataset and print one of those.
LSA = myLSA(); profiles = readtable('online_profiles.xlsx'); fprintf('%s\n%s\n%s\n%s\n%s\n',profiles.Profile{1}(1:73),... profiles.Profile{1}(74:145),profiles.Profile{1}(146:219),... profiles.Profile{1}(220:291),profiles.Profile{1}(292:358))
Working at a coffee shop adventures tacos medical school. Feminism going to the gym strong and confident Family Guy listening to music, my beard Kurosawa discussing politics trying different restaurants I know I listed more than 6 things. Snowboarding no drama outdoor activities discussing politics pickles my friends tell me they don't get why I'm single.
Not bad for a random word salad, except that they are all male profiles. If you need female profiles, you need to find other sources.
Text Processing Pipeline
Before we can analyze text, we need to process it into an appropriate form. There is a fairly standard process for English text.
- Tokenization: split text into word tokens using white space, etc.
- Standardization: standardize word forms, i.e., all lowercase
- Stopwords: remove common words, such as ‘the, a, at, to’
- Stemming: reduce words into their root forms by trimming their endings
- Indexing: sort the words by document and count word frequencies
- Document-Term Frequency Matrix: turn indexed frequency counts into a document x term matrix
The tokenizer method takes care of the first four steps – tokenization, normalization, stopwords and stemming. Check out the before and after.
tokenized = LSA.tokenizer(profiles.Profile);
before = profiles.Profile(1)
after = {strjoin(tokenized{1},' ')}
before =
'Working at a coffee shop adventures tacos medical school. Feminism goi...'
after =
'work coffe shop adventur taco medic school femin go gym strong confid ...'
Next, the indexer method creates word lists and word count vectors.
[word_lists,word_counts] = LSA.indexer(tokenized);
Then we create a document-term frequency matrix from these using docterm. The minimum frequency is set to 2 and that drops any words that only occur once through the entire collection of documents.
docterm = LSA.docterm(word_lists,word_counts,2);
TF-IDF Weighting
You could use the document-term frequency matrix directly, but raw word count is problematic – it gives too much weight to frequent words, and frequent words that appear in many documents are usually not so useful to understand the differences among those documents. We would like to see the weight to represent the relevancy of each word.
TF-IDF is a common method for frequency weighting. It is made up of TF, which stands for Term Frequency, and IDF, Inverse Document Frequency. TF scales based on the number of times a given term appears in a document, and IDF inversely scales based on how many document a given term appears in. The more frequently a word appears in documents, the less weight it gets. TF-IDF is just a product of those two metrics. Let’s use tfidf to apply this weighting scheme. It also optionally returns TF.
tfidf = LSA.tfidf(docterm);
I went through each step of text processing, but we could instead run vectorize to turn a raw cell array of online dating profiles into a TF-IDF weighted matrix in one shot.
tfidf = LSA.vectorize(profiles.Profile,2);
Low-Rank Approximation
Once the data is transformed into a matrix, we can apply linear algebra techniques for further analysis. In LSA, you typically apply singular value decomposition (SVD) to find a low-rank approximation.
Let’s first get the components of SVD. U is the SVD document matrix, V is the SVD term matrix, and S is the singular values.
[U,S,V] = svd(tfidf);
If you square S and divide it by sum of S squared, you get the percentage of variance explained. Let’s plot the cumulative values.
explained = cumsum(S.^2/sum(S.^2)); figure plot(1:size(S,1),explained) xlim([1 30]);ylim([0 1]); line([5 5],[0 explained(5)],'Color','r') line([0 5],[explained(5) explained(5)],'Color','r') title('Cumulative sum of S^2 divided by sum of S^2') xlabel('Column') ylabel('% variance explained')

You see that the first 5 columns explain 60% of variance. A rank-5 approximation will retain 60% of the information of the original matrix. The myLSA class also provides lowrank that performs SVD and returns a low rank approximation based on some criteria, such as number of columns or the percentage of variance explained.
[Uk,Sk,Vk] = LSA.lowrank(tfidf,0.6);
Visualize Online Dating Profiles
We can also use the first 2 columns to plot the SVD document matrix U and SVD term matrix V in 2D space. The blue dots represent online dating profiles and words around them are semantically associated to those profiles.
figure() scatter(U(:,1), U(:,2),'filled') title('Online Dating Profiles and Words') xlabel('Dimension 1') ylabel('Dimension 2') xlim([-.3 -.03]); ylim([-.2 .45]) for i = [1,4,9,12,15,16,20,22,23,24,25,27,29,33,34,35,38,47,48,53,57,58,... 64,73,75,77,80,82,83,85,88,97,98,103,113,114,116,118,120,125,131,... 136,142,143,156,161,162,166,174,181,185,187,199,200,204,206,212,... 234,251] text(V(i,1).*3, V(i,2).*3, LSA.vocab(i)) end text(-0.25,0.4,'Wholesome/Sporty','FontSize', 12, 'Color', 'b') text(-0.15,-0.15,'Bad Boy/Colorful','FontSize', 12, 'Color', 'b')
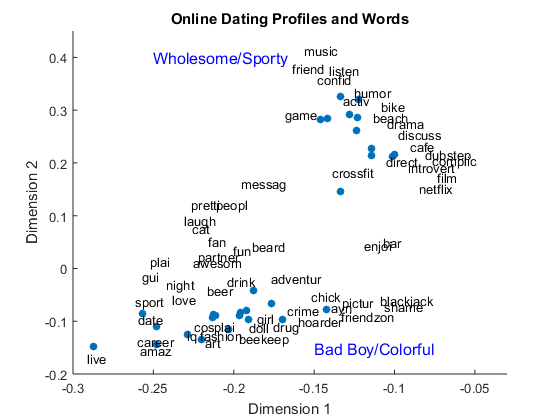
You can see there are two main clusters – what I would call the “Wholesome/Sporty” cluster and one called the “Bad Boy/Colorful” cluster, based on the words associated with them. This makes sense, because Lauren provides two options in her profile generator:
- Typical inane jabber
- With a side of crazy sauce
Can you guess which cluster belongs to which category?
Now you can cluster a whole bunch of profiles at once and quickly eliminate those that don’t match your taste. You can also add your own profile to see which cluster you belong to, and, if that puts you in a wrong cluster of profiles, then you may want to update your profile.
Computing Similarity
Say you find a cluster of profiles you are interested in. Among the profiles you see there, which one is the closest to your taste? To answer this question, we need to find a way to define the similarity of two documents. If you use the Euclidean distance between vectors, the longer documents and shorter documents can have very different values even if they share many of the same words. Instead, we can use the angle between the vectors to determine the similarity. This is known as Vector Space Model. For ease of computation, cosine is used for similarity computation.
cosine = dot(A,B)/(norm(A)*norm(B))
The greater the value, the closer (= similar).
Angle Cosine ___________ ______ 0 degree 1 90 degrees 0 180 degrees -1
For practical implementation, you can just length normalize vectors by the L2 norm, and compute the dot product.
cosine = dot(A/norm(A),B/norm(B))
You can apply length normalization ahead of the similarity computation. We will use the rank-5 approximation of the SVD document matrix to compare online dating profiles using normalize.
doc_norm = LSA.normalize(U(:,1:5));
Now we can compute cosine similarities between profiles with score. Let’s compare the first profile to the first five profiles.
LSA.score(doc_norm(1:5,:),doc_norm(1,:))
ans =
1
0.20974
0.55248
0.97436
0.72994
The first score is 1, which means it is a perfect match, and that’s because we are comparing the first profile to itself. Other profiles got lower scores depending on how similar they are to the first profile.
Getting the Ranked Matches
It’s probably useful if you can describe your ideal date and find the profiles that match your description ordered by similarity. It is a bit like a search engine.
To compare the new text string to the pre-computed matrix, we need to apply the same pre-processing steps that we have already seen. query can take care of the tedious details.
q = 'someone fun to hang out with, good sense of humor, likes sushi,'; q = [q 'watches Game of Thrones, sees foreign films, listens to music,']; q = [q 'do outdoor activities or fitness']; weighted_q = LSA.query(q);
Now we need to transform the query vector into the rank-5 document space. This is done by transforming M = U*S*V' into U = M'*V*S^-1 and substituting M' with the query vector and V and S with their low rank approximations.
q_reduced = weighted_q * V(:,1:5) * S(1:5,1:5)^-1;
The myLSA class also provides the reduce method to perform the same operation.
q_reduced = LSA.reduce(weighted_q);
Then we can length-normalize the query vector and compute the dot products with documents. Let’s sort the cosine similarities in descending order, and check the top 3 results.
q_norm = LSA.normalize(q_reduced); [scores,idx] = sort(LSA.score(doc_norm,q_norm),'descend'); disp('Top 3 Profiles') for i = 1:3 profiles.Profile(idx(i)) end
Top 3 Profiles
ans =
'Someone who shares my sense of humor fitness my goofy smile Oxford com...'
ans =
'My cats I'm really good at my goofy smile mountain biking. Fixing up m...'
ans =
'My eyes just looking to have some fun if you think we have something i...'
Looks pretty reasonable to me!
In this example, we applied TF-IDF weighting to both the document-term frequency matrix as well as the query vector. However, you only need to apply IDF just once to the query to save computing resources. This approach is known as lnc.ltc in SMART notation system. We already processed our query in ltc format. Here is how you do lnc for your documents – you use just TF instead of TF-IDF:
[~, tf] = LSA.vectorize(profiles.Profile,2); doc_reduced = LSA.lowrank(tf,0.6); doc_norm = LSA.normalize(doc_reduced);
What about Japanese Text?
Can my Japanese friends benefit from this technique? Yes, definitely. Once you have the document-term frequency matrix, the rest is exactly the same. The hardest part is tokenization, because there is no whitespace between words in Japanese text.
Fortunately, there are free tools to do just that – they are called Japanese Morphological Analyzers. One of the most popular analyzers is MeCab. A binary package is available for installation on Windows, but it is for 32-bit, and doesn’t work with MATLAB in 64-bit. My Japanese colleague, Takuya Otani, compiled the source code to run it on MATLAB 64-bit on Windows.
MATLAB provides an interface to shared libraries like DLLs, and we can use loadlibrary to load them into memory and access functions from those shared libraries. Here is an example of how to call the shared library libmecab.dll that Takuya compiled.
You may not have any particular need for handling Japanese text, but it gives you a good example of how to load a DLL into MATLAB and call its functions. Please note some requirements in case you want to try:
- Have a 64-bit Japanese Windows computer with 64-bit MATLAB
- Have a MATLAB-compatible compiler installed and enabled on your computer
- Follow Takuya’s instructions to compile your own 64-bit DLL and place it in your current folder along with its header file.
loadlibrary('libmecab.dll', 'mecab.h');
When you run this command, you may get several warnings, but you can ignore them. If you would like to see if the library was loaded, use libfunctionsview function to view the functions available in the DLL.
libfunctionsview('libmecab')
To call a function in the DLL, use calllib. In the case of Mecab, you need to initialize Mecab and obtain its pointer first.
argv = libpointer('stringPtrPtr', {'MeCab'}); argc = 1; mecab = calllib('libmecab', 'mecab_new', argc, argv);
As an example, let’s call one of the Mecab functions you can use to analyze Japanese text – mecab_sparse_tostr.
text = 'Some Japanese text'; result = calllib('libmecab', 'mecab_sparse_tostr', mecab, text);
When finished, clear the pointer and unload the DLL from the memory using unloadlibrary.
clearvars mecab unloadlibrary('libmecab')
Call for Action
If you happen to be single and are willing to try the experiment described in the New York Times article, please report back here with your results. The New York Times now provides a free app to generate 36 magical questions!
Published with MATLAB® R2015a
- Category:
- Big Data,
- Fun,
- Statistics,
- Strings
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.