Errorbar with Adjusted Tick Size
Jiro's pick this week is Errorbar with Adjusted Tick by Arnaud Laurent.
Just this week, I got a comment from Felipe on a guest post ("Making Pretty Graphs") that I did on Loren's blog. He pointed out this function by Arnaud that helps adjust the size of the horizontal ticks at the top and bottom of the errorbars that I had to fix manually in the post. Thanks Felipe for the tip!
The errorbar automatically determines the tick size based on the limits of the axes, and there is no simple option to change that. However, the function can return a handle to errorbarseries, and you can modify the tick size by digging into its properties. That's what I did in my blog post. Now, it's even easier with Arnaud's errorbar_tick. I echo Felipe's comment on the entry page that it's nice how errorbar_tick works on the handle returned by the errorbar function, rather than recreating the functionality available in errorbar.
Create a standard errorbar plot:
x = 1:10; y = sin(x); e = std(y)*ones(size(x)); h = errorbar(x,y,e, 'o-'); set(h, 'MarkerSize', 10, 'MarkerFaceColor', [.3 1 .3], ... 'MarkerEdgeColor', [0 .5 0]);
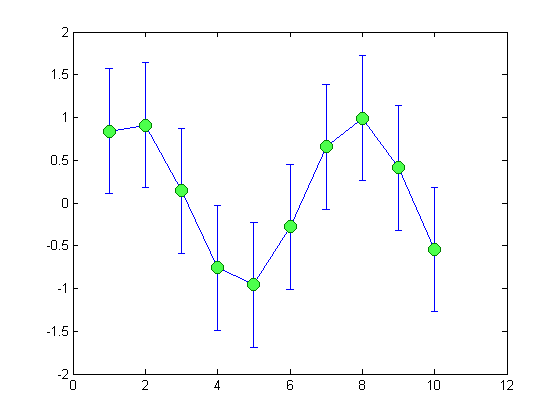
Apply errorbar_tick to increase tick size:
errorbar_tick(h, 30);

Comments
Let us know what you think here or leave a comment for Arnaud.
- Category:
- Picks
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.