The OEIS and the Recamán Sequence
Here are the first 12 integers from an infinite sequence defined by a deceptively simple rule. Can you see the pattern? Try to predict the next number in the sequence.
0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22
Contents
OEIS
The OEIS, the On-Line Encyclopedia of Integer Sequences, is a mathematical treasure chest. Established in 1964 by Neal J. A. Sloan, the OEIS has over 300,000 entries. Dozens are added each week. Anyone who registers can propose a new entry. A team of 130 volunteer editors then review the proposals and create new entries.
A powerful search engine accepts queries made from short subsequences and finds all the entries in the encyclopedia that contain that query. It's similar to a search engine that identifies a piece of music from a few notes.
Here is the link, https://oeis.org. One way to introduce yourself to the OEIS is to take a look at https://oeis.org/OEIS_pics.html. Or, watch the OEIS movie on YouTube, https://www.youtube.com/watch?v=LCWglXljevY.
A005132
Did you try to guess the next number is our sequence yet? You can ask the OEIS. If you enter the 12 numbers in the search window, you get something like this.
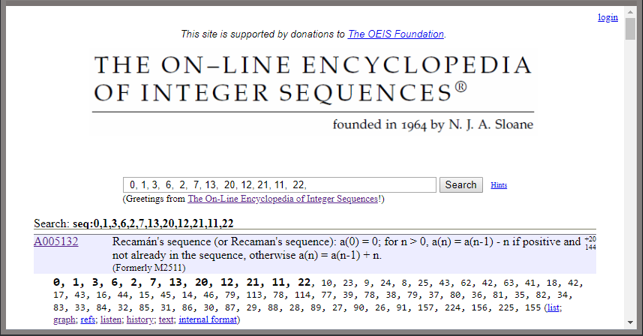
So, you can see that the next number is 10.
Each entry in the encyclopedia has an identifier; for this sequence the identifier is A005132. We could also reach A005132 by searching for "A005132" or "Recaman".
Neal Sloan has said this is one of his favorite sequences in the entire collection. He learned about it in a 1991 letter from Columbian mathematician Bernardo Recamán Santos.
In the past few weeks I've become infatuated with Recamán sequence.
The rule
Starting with $a_0$ = 0, the sequence is generated by the recurrence
$$a_n = a_{n-1} \pm n$$
The minus sign is preferred. It is used if the resulting $a_n$ is positive and not already in the sequence; otherwise the plus sign is used.
So, for n = 1, 2, 3 the plus sign is required and the rule generates the familiar triangle numbers 1, 3, 6. But when n = 4 it is possible to use the minus sign because
$a_4$ = $a_3$ - 4 = 6 - 4 = 2
is not already in the sequence.
recaman.m
Here is my MATLAB function.
type recaman
function R = recaman(m)
% R = recaman(n) is the first n terms of Recamán's sequence.
% OEIS A005132, https://oeis.org/A005132.
a = 0;
R = a;
for n = 1:m-1
if a > n && ~ismember(a-n,R)
a = a-n;
else
a = a+n;
end
R(n+1) = a;
end
end
It turns out to be faster for the sequence array R to grow during the recurrence than it is to preallocate it with R = zeros(1,m).
n = 12
Let's visualize the Recamán sequence. A plot made with semicircles connecting the terms is especially illuminating. The first small semicircle, on the left, has diameter one and end-points at the first two elements, 0 and 1. Subsequently, the diameter of the n-th semicircle is n and its end-points are $a_{n-1}$ and $a_n$. This plot ends on the right at $a_{12}$ = 22
I learned about this way of plotting the Recamán sequence from the YouTube channel Numberphile in a video featuring Alex Bellos and Edmund Harriss.
set(gcf,'position',[200 200 480 360])
n = 12;
recaman_circles(n)

A conventional MATLAB plot of the sequence versus index is also worth a look. The title is the last term, $a_n$.
recaman_plot(n)

n = 66
The value n = 66 is a good stopping point for the plots. The next value would jump from $a_{66}$ = 91 to $a_{67}$ = 157.

The line plot is showing its characteristic behavior -- stretches of sawtooth oscillation with increasing amplitude separated by chaotic jumps to new "energy levels".

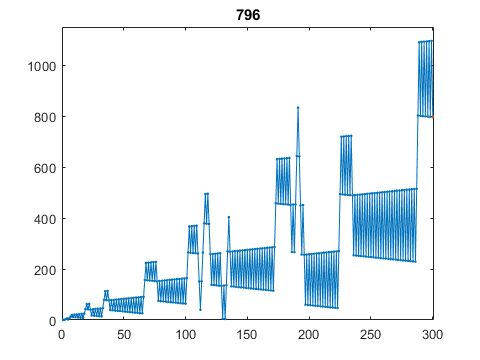
n = 300
This behavior with 300 terms continues indefinitely.
n = 300; recaman_plot(n)
Complexity
The computational complexity of recaman(n) is O(n^2). It takes about six minutes to generate a million terms on my laptop.
Every integer?
The Recamán recurrence is designed to hit every positive integer. Does it succeed? For each k > 0, is there a value of n for which $a_n$ = k. This is an open question. Sometimes n has to be surprisingly large.
Take k = 4.
k = 4 R = recaman(1000); n = find(k == R)
k =
4
n =
132
Take k = 19.
k = 19 R = recaman(100000); n = find(k == R)
k =
19
n =
99735
Take k = 852655. Wait, don't try that. Nobody knows if the sequence ever hits this value. Benjamin Chaffin has computed 10^230 terms without seeing 852655.
Music
I can't easily include audio in my blog. You'll have to do it yourself. For a real treat, go to https://oeis.org/A005132 and click on "listen".
Another sequence
Let's have a little more fun with the OEIS. There are only a handful of people in the world that know the next term in this sequence.
9, 6, 3, 9, 7, 2, 3, 8
To find out, enter these numbers in the search window at https://oeis.org. Or, bring up your MATLAB and
edit membrane
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.