Amaze, A Maze Generator
My MATLAB® program, amaze, generates mazes by combining old friends, numgrid and delsq, with a new friend, the graph object. Let's see how we make this example maze.
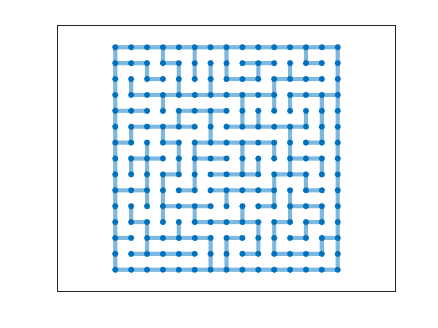
Contents
Beginnings
Select a maze size. Our example is 15-by-15.
n = 15;
We are going to make two graphs, the barriers and the cells. The barriers, B, is the graph of the classic five-point discrete Laplacian on an n-by-n square grid. Each node is the interior is connected to its four closest neighbors and each node on the boundary has two or three neighbors. The functions delsq and numgrid have been in the sparfun directory since sparse matrices were introduced in 1992. The graph object was introduced in R2015b. We are going to carve a path through this grid.
Db = delsq(numgrid('S',n+2)); B = graph(logical(Db),'omitselfloops');

The cells, C, are also based on the five-point discrete Laplacian, but on an (n-1)-by-(n-1) grid. Initially C has just the nodes, no edges. When we plot B and C together, the nodes of C are centered in the squares of B.
m = n-1;
Dc = delsq(numgrid('S',m+2));
C = graph(logical(Dc),'omitselfloops');

Random walks
available = 1:m^2; % Nodes we haven't visited yet. branches = []; branching = 'middle'; tree = zeros(0,2); % Depth first search. p = 1;
Now we make a series of random walks on C.
while true % Break when available is empty
available(p) = 0;
if ~any(available)
break
end
Each step is from a node to a random choice of one of its neighbors that has not already been visited.
[~,~,ngh] = find(available(neighbors(C,p)));
if ~isempty(ngh)
idx = randi(length(ngh)); % Random choice. q = ngh(idx); % Next cell. tree(end+1,:) = [p q];
At the same time, the edge in the barrier B that is blocking the step is removed.
[i,j] = wall(p,q);
B = rmedge(B,i,j);
We keep a list of the nodes where a random choice between two or three neighbors is made.
if length(ngh) > 1 branches(end+1) = p; end p = q;
Eventually the walk reaches a dead end, a node whose neighbors have all been visited. Here is the first such walk in our example.

Backtrack
When we reach a dead end, we backtrack to one of the nodes on our list of nodes where we had a choice of available neighbors. Here another kind of choice is made. We can go back to the first node on the list, to the node in the middle of the list, or to the last node on the list.
else switch branching case 'first' idx = 1; case 'last' idx = length(branches); otherwise idx = round(length(branches)/2); end p = branches(idx); branches(idx) = []; end
Here is the result of backtracking to the middle and then walking to a second dead end.

Here is the result after several more backtracks.

end
C = graph(tree(:,1),tree(:,2));
Near the end of this process, the length of a path before a dead end and a backtrack becomes shorter and shorter. A path may involve a single point. Eventually all the nodes in C are covered. Here is the final result.

When the entire path is plotted with linestyle = 'none' we have the maze.

Shortest path
We can easily "solve" the maze by asking for the shortest path from one corner to another.
path = shortestpath(C,1,m^2);
(Exercise: How does the branching parameter affect the average length of this path?)

Animation

Software
I have a program called amazing that allows you to investigate amaze. I've submitted it to the MATLAB Central File Exchange and will put the link here. I will also add amazing to version 4.40 of Cleve's Laboratory.
Thanks
Thanks to Pat Quillen who provided invaluable help.









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.