Mount St. Helens and Matrix Rank
What do Mount St. Helens and the rank of a matrix have in common? The answer is the MATLAB function peaks. Let me explain. Please bear with me -- it's a long story.
Contents
Mount St. Helens

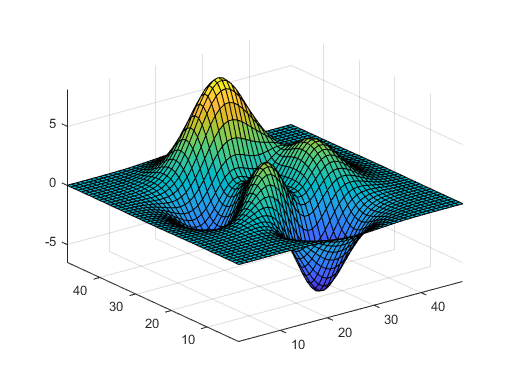
Mount St. Helens is an active volcano in the Cascade Range near Portland, Oregon and Seattle, Washington. She had a dramatic eruption in May 1980. Four years after the eruption, I moved to Beaverton, Oregon to join a spinoff from Intel that was developing one of the world's first commercial parallel computers, the iPSC. In Beaverton, I met two guys from Tektronix, a company famous for oscilloscopes that was then trying to get into computer graphics. These guys, whose names I don't remember, were plotting a surface that resembled Mount St Helens. That surface eventually became the MATLAB function peaks, which is a function of two variables that is useful for demonstrating surf, mesh, pcolor and contour.
small_fig
clear
P = peaks;
surf(P)
axis tight
Rank Revealing Factorizations
Two months ago, I wrote a blog post about rank revealing matrix factorizations, It is hard to think of the array P that we obtain from peaks as the representation of a linear transformation and a test matrix, but it is. In fact, for any positive integer n, peaks(n) is an n -by- n matrix. The default has n = 49.
I was very surprised when I discovered that for any n > 2, the rank of peaks(n) is only 3.
rankP = rank(P)
rankP =
3
C*inv(W)*R
MATLAB's rank counts nonzero singular values, but we can also try the factorization P = C*inv(W)*R. We intend to use car only on small matrices that have integer entries. This P is neither small nor integer, but that doesn't stop us. car also finds the rank is 3.
[C,W,R] = car(P); whos
Name Size Bytes Class Attributes C 49x3 1176 double P 49x49 19208 double R 3x49 1176 double W 3x3 72 double rankP 1x1 8 double
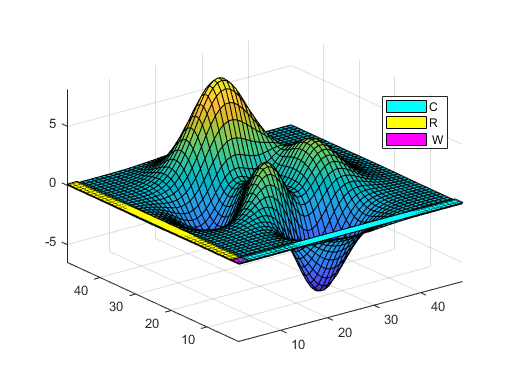
The 49-by-3 matrix C is the first three columns of P and the 3-by-49 matrix R is the first three rows of P. The 3-by-3 matrix W is their intersection, P(1:3,1:3). These three matrices lie safely out of the reach of volcanic eruptions. Here they are, in color.
d = .1; n = 49; r = 3; s = [patch([1-d n+d n+d 1-d 1-d],[1-d 1-d r+d r+d 1-d],[d d d d d],'c') patch([1-d r+d r+d 1-d 1-d],[1-d 1-d n+d n+d 1-d],[d d d d d],'y') patch([1-d r+d r+d 1-d 1-d],[1-d 1-d r+d r+d 1-d],[d d d d d],'m')]; legend(s,{'C','R',' W'}, 'position',[.75 .62 .12 .12]);
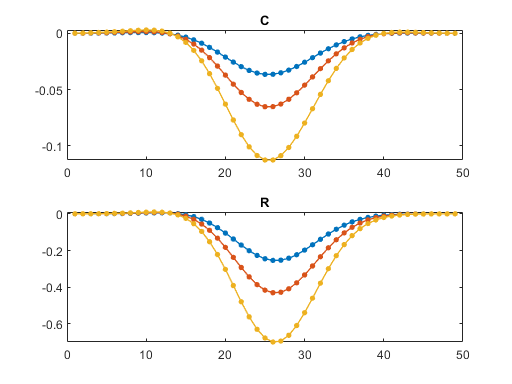
Plots of C and R do not easily reveal the fact that they contain enough information to reconstruct the entire surface P.
subplot(2,1,1) plot(C,'.-','linewidth',1,'markersize',12) title('C') subplot(2,1,2) plot(R','.-','linewidth',1,'markersize',12) title('R')
peaks
The function peaks begins by generating matrices x and y that sample a continuous real variable on the interval [-3,3]. Setting the meshsize dx = 1/8 leads to n = 49. Smaller mesh sizes lead to larger matrices, but they all have rank 3.
dx = 1/8; [x,y] = meshgrid(-3:dx:3);
The core of peaks is this formula, which must be something like the one that the Tektronix guys were using for their Mt. St. Helens It is not obvious that the formula always generates a matrix of low rank.
z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ... - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ... - 1/3*exp(-(x+1).^2 - y.^2);
Rank
The rest of this post is devoted to proving that rank(z) = 3.
Here are two important facts about the rank of sums and pointwise products.
- rank(A + B) <= rank(A) + rank(B)
- rank(A.*B) <= min(rank(A),rank(B))
In particular, if A and B are both rank one, then
- rank(A + B) <= 2
- rank(A.*B) <= 1
Reformulate
Let's factor out the exponentials using this function.
E = @(x,a) exp(-(x+a).^2);
So, here is z again.
z = 3*(1-x).^2.*E(x,0).*E(y,1) ... - 10*(x/5 - x.^3 - y.^5).*E(x,0).*E(y,0) ... - 1/3.*E(x,1).*E(y,0);
Let z1 be the first term.
z1 = (3*(1-x).^2).*E(x,0).*E(y,1);
rank(z1) = 1 because z1 is the pointwise product of three matrices. There is no sum.
Let
zx = -10*(x/5 - x.^3).*E(x,0) - 1/3.*E(x,1); zy = (10*y.^5).*E(x,0);
rank(zx) = 1 because zx does not involve y.
rank(zy) = 1 because zy is a pointwise product.
z2 = (zx + zy).*E(y,0);
rank(z2) = (1 + 1)*1 = 2
z = z1 + z2;
rank(z) = 1 + 2 = 3
Check
My original P is still in the workspace.
check = norm(P - z,inf)
check = 1.3517e-14








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.