Redheffer and Mertens, Accelerated
Shortly after I published the second post about the Mertens conjecture, a reader's comment suggested a new approach to computing Redheffer determinants and the Mertens function. It is now possible to compute a half-million values of the Mertens function in about five hours.
Contents
Block matrices
The comment references the Wikipedia article on block matrices.
You could also consider the matrix as a 2x2 block matrix and
use the formula for the determinant of a block matrix [1].
A = redheffer(n);
M = full(A(1,1) - A(1, 2:end) * (A(2:end,2:end) \ A(2:end, 1)));
Since the (n-1)x(n-1) block is upper triangular, the solve becomes
a back-substitution.
redmert
My new program is named redmert, an abbreviation of Redheffer-Mertens. It uses the fact that redheffer(n) is obtained from redheffer(n-1) by appending the last column.
Let R(n) denote the upper or right-triangular part of redheffer(n).
R(n) = triu(redheffer(n))
R(n) is sparse, upper triangular and has ones on the diagonal. The indices of the nonzeros in the last column of R(n) are the factors of n. For example, here is R(8).
R8 = full(triu(redheffer(8)))
R8 =
1 1 1 1 1 1 1 1
0 1 0 1 0 1 0 1
0 0 1 0 0 1 0 0
0 0 0 1 0 0 0 1
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1
The idea behind redmert is to compute a sequence of Redheffer matrices, R, and associated values of the Mertens function, M.
[M,R] = redmert(p,R)
The input is a scalar integer p, the desired sequence length, and a sparse matrix R, the upper triangle of a Redheffer matrix of some order, n. The output is an integer vector of values M(n+1:n+p) and the upper triangle of the Redheffer matrix of order n+p. This output R can then be used as the input R in another call to redmert.
The sequence is started with an empty R.
For example,
[M,R] = redmert(8,[]);
The output is mertens(n), n = 1:8, and R8 from the example above.
MR8 = full(R)
M =
1
0
-1
-1
-2
-1
-2
-2
R8 =
1 1 1 1 1 1 1 1
0 1 0 1 0 1 0 1
0 0 1 0 0 1 0 0
0 0 0 1 0 0 0 1
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1
Inside redmert
The entire code for redmert is twelve lines long. It manipulates sparse matrices and uses sparse backslash to solve a triangular system. Nothing else is required.
Lines 7 and 8 generate the last column of R and lines 9 and 10 implement the new idea about block matrices.
dbtype redmert
1 function [M,R] = redmert(p,Rin) 2 M = zeros(p,1); 3 R = sparse(triu(Rin)); 4 n = size(R,1); 5 for q = 1:p 6 n = n+1; 7 k = (mod(n,1:n) == 0); 8 R(k,n) = 1; 9 e = ones(n-1,1); 10 M(q) = R(1,1) - e'*(R(2:n,2:n)\e); 11 end 12 end
mertens_plot
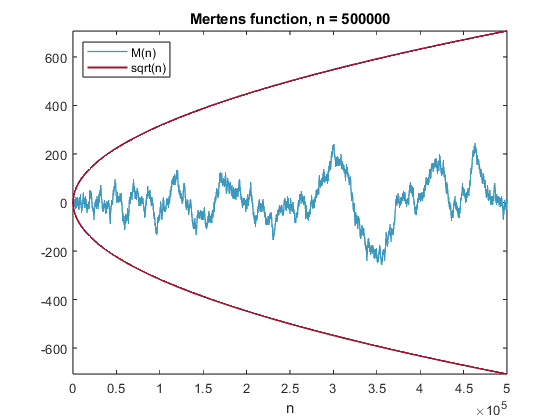
It takes about five hours for redmert to compute half a million values on my laptop.
n = 0.5e6;
p = 0.5e4;
R = sparse([]);
M = [];
for k = p:p:n
disp(k)
[Mout,R] = redmert(p,R);
M = [M; Mout];
mertens_plot(M)
end
mertens_plot
Postscript
I started this project by being surprised to find myself computing determinants. Now I am back to my long-time position disparaging determinants. They have been replaced by a good friend, backslash.








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.