
I am giving a five-minute talk today, May 26, at the virtual seminar on Complexity of Matrix Computations. Here are my slides. Two new MATLAB functions, tred and imtql, instrumented to count flops, are available in symeig.m.... 更多内容 >>

I am giving a five-minute talk today, May 26, at the virtual seminar on Complexity of Matrix Computations. Here are my slides. Two new MATLAB functions, tred and imtql, instrumented to count flops, are available in symeig.m.... 更多内容 >>
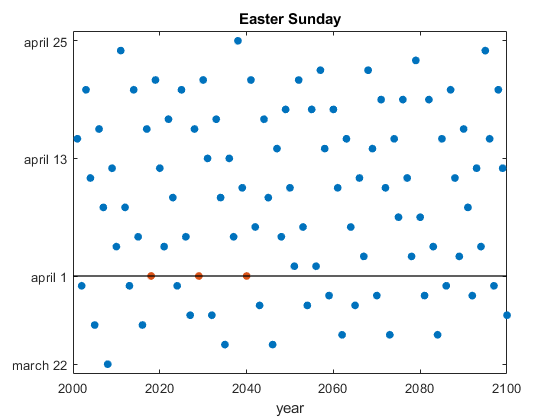
What do the years 2018, 2029 and 2040 have in common? They are the only years in the 21st century when Easter Sunday occurs on April Fools Day.... 更多内容 >>

Recently, I had email from a student in Italy.... 更多内容 >>

This post is by my colleague Cosmin Ionita.... 更多内容 >>

This week’s post is by Reece Teramoto.
MathWorks recently took over sponsorship of the Math Modeling Challenge, a contest for high school juniors and seniors in the U.S organized by SIAM – Society... 更多内容 >>

Find the optimum traveling salesman tour through the capitals of the 48 contiguous states in the USA.... 更多内容 >>

Today is Easter Sunday. Why? How is the date of Easter determined?... 更多内容 >>

Three-term recurrence relations are the basis for computing Bessel functions. Contents A Familiar Three-Term Recurrence Friedrich Bessel Bessel Functions Miller's Algorithm ... 更多内容 >>
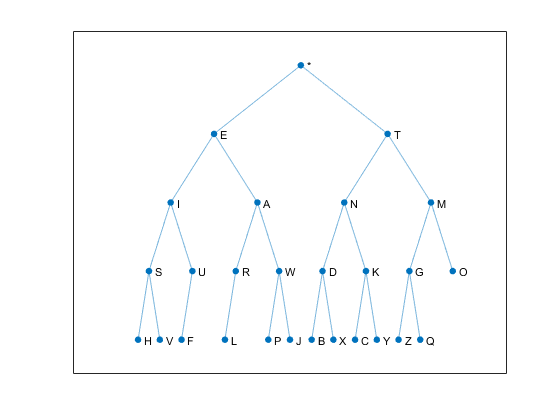
A binary tree is an elegant way to represent and process Morse code. The new MATLAB graph object provides an elegant way to manipulate binary trees. A new app, morse_tree, based on this approach, is now available in version 2.40 of Cleve's Laboratory.... 更多内容 >>

MIT's Professor Daniel Frey recently introduced me to an ancient mechanical puzzle known as "Chinese Rings", "Patience", or "Baguenaudier." I have modified Daniel's simulator to produce a new app. The state space of the puzzle forms a hypercube.... 更多内容 >>