This post is by my colleague Cosmin Ionita.... read more >>

This week’s post is by Reece Teramoto.
MathWorks recently took over sponsorship of the Math Modeling Challenge, a contest for high school juniors and seniors in the U.S organized by SIAM – Society... read more >>

Find the optimum traveling salesman tour through the capitals of the 48 contiguous states in the USA.... read more >>

Today is Easter Sunday. Why? How is the date of Easter determined?... read more >>

Three-term recurrence relations are the basis for computing Bessel functions. Contents A Familiar Three-Term Recurrence Friedrich Bessel Bessel Functions Miller's Algorithm ... read more >>

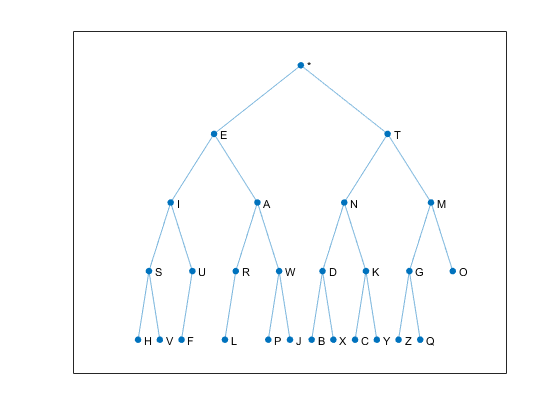
A binary tree is an elegant way to represent and process Morse code. The new MATLAB graph object provides an elegant way to manipulate binary trees. A new app, morse_tree, based on this approach, is now available in version 2.40 of Cleve's Laboratory.... read more >>

MIT's Professor Daniel Frey recently introduced me to an ancient mechanical puzzle known as "Chinese Rings", "Patience", or "Baguenaudier." I have modified Daniel's simulator to produce a new app. The state space of the puzzle forms a hypercube.... read more >>

"ULP" stands for "unit in the last place." An ulps plot samples a fundamental math function such as $\sin{x}$, or a more esoteric function like a Bessel function. The samples are compared with more accurate values obtained from a higher precision computation. A plot of the accuracy, measured in ulps, reveals valuable information about the underlying algorithms.... read more >>

A headline in the New York Times at the end of 2016 said "Growth of U.S. Population Is at Slowest Pace Since 1937". This prompted me to revisit an old chestnut about fitting and extrapolating census data. In the process I have added a couple of nonlinear fits, namely the logistic curve and the double exponential Gompertz model.... read more >>

This is a follow-up to my previous follow-up, posted several days ago. A very careful reader, Bruno Bazzano, contributed a comment pointing out what he called "a small typo" in my code for the classic Gram-Schmidt algorithm. It is more than a small typo, it is a serious blunder. I must correct the code, then do more careful experiments and reword my conclusions.... read more >>