Morse Code, Binary Trees and Graphs
A binary tree is an elegant way to represent and process Morse code. The new MATLAB graph object provides an elegant way to manipulate binary trees. A new app, morse_tree, based on this approach, is now available in version 2.40 of Cleve's Laboratory.
Contents
EXM chapter
I have a chapter on Morse Code and binary trees in Experiments with MATLAB. Some of this blog post is taken from that chapter. But today's implentation is much more, as I said, elegant. In EXM I represented a binary tree as a cell array of cell arrays. Now I am using clever indexing into a linear character string, together with the MATLAB graph object. The resulting code is much shorter and more readable.
Binary trees
Here's all we have to do to get a picture of a binary tree. First we create the adjacency matrix and view its spy plot.
n = 31; j = 2:n; k = floor(j/2); A = sparse(k,j,1,n,n); spy(A)

Then we create and plot the directed graph. The MATLAB digraph object, and its supporting plot method, are doing all of the work.
G = digraph(A); Gp = plot(G); set(gca,'xtick',[],'ytick',[])

This is the complete binary tree with five levels, and consequently $2^5-1$ nodes. (In defiance of nature, computer scientists put the root of a tree at the top.)
Follow the nodes in numerical order, from top to bottom and left to right. You are doing a breadth first traversal of the structure. The successors of the node with index j have indices 2j and 2j+1. This makes old-fashioned linear indexing possible.
I want to save the coordinates of the nodes for use in the layout in my next plot.
x = Gp.XData; y = Gp.YData;
Morse code
Morse code is no longer important commercially, but it still has some avid fans among hobbyists. Morse code was invented over 150 years ago, not by Samuel F. B. Morse, but by his colleague, Alfred Vail. It has been in widespread use ever since. The code consists of short dots, '.', and longer dashes, '-', separated by short and long spaces. You may be familiar with the international distress signal, '... --- ...', the code for "SOS", abbreviating "Save Our Ships" or perhaps "Save Our Souls". But did you notice that some modern cell phones signal '... -- ...', the code for "SMS", indicating activity of the "Short Message Service".
Until 2003, a license to operate an amateur radio in the US required minimal proficiency in Morse code. When I was in junior high school, I learned Morse code to get my ham license, and I've never forgotten it.
According to Wikipedia, in 2004, the International Telecommunication Union formally added a code for the ubiquitous email character, @, to the international Morse code standard. This was the first addition since World War I.
Morse tree
I could provide a table showing that '.-' is the code for A, '-...' the code for B, and so on. But I'm not going to do that, and my MATLAB program does not have such a table. As far as I am concerned, Morse code is defined by a MATLAB statement containing the 26 upper case letters of the English language, an asterisk, and four blanks.
morse = '*ETIANMSURWDKGOHVF L PJBXCYZQ ';
The asterisk at the start serves as the root of the tree. The four blanks will correspond to four missing nodes in the bottom level of the tree. So the binary tree is not going to be complete. The automatic layout in the graph/plot method does not draw a perfect tree. This is why I saved the node coordinates from the plot of the full tree. Let's remove the rows and columns of these potentially unlabeled nodes from the adjacency matrix, and the coordinates.
m = find(morse == ' ');
A(:,m) = [];
A(m,:) = [];
x(m) = [];
y(m) = [];
Convert the character array into a cell array of individual chars.
nodes = num2cell(morse);
nodes(m) = '';
Create the directed graph with these node labels.
G = digraph(A,nodes);
Plot the graph, using the layout saved from the full tree.
plot(G,'xdata',x,'ydata',y, ... 'showarrows','off'); set(gca,'xtick',[],'ytick',[])
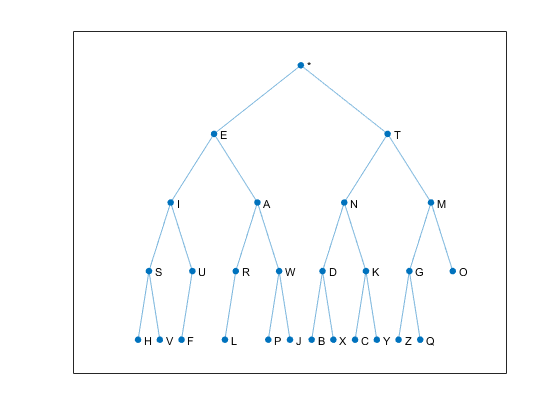
If you follow the links downward and emit a dot when you go left and a dash when you go right, you have Morse code. For example start at the root, go left once, then right once. You will reach A and will have generated '.-', the code for A.
Morse code is already present in the defining character vector morse, even before we create and plot a graph. The character with index 5 is A. The characters with indices 2*5 and 2*5+1 are R and W.
j = 5;
morse(j)
morse(2*j:2*j+1)
ans =
'A'
ans =
'RW'
Consequently, the Morse code for R and W is '.-.' and '.--'. This works everywhere in the first half of morse. The characters in the second half don't (yet) have successors.
Extensions
Morse code can be extended by replacing the blanks in the basic tree with characters that are not in the 26 letter English alphabet and adding two more levels to the tree. Several different extensions have been in use at different times and different regions of the world. The Wikipedia page for Morse code includes a binary tree with some commonly used extensions. The fifth level includes the 10 decimal digits, several non-Latin chacters, and a few punctuation marks. The sixth level includes several punctuation marks.
morse_tree app
Here is a screen shot from the new app, morse_tree, that is available in version 2.40 of Cleve's Laboratory. Clicking on the toggle labeled "extend" shows two more levels of the tree and some extensions, although not many as Wikipedia's tree. Clicking on a node in our tree highlights that node while the sound of the corresponding code is played. This screen shot shows A highlighted.
Text entered in the box below the tree will be encoded and the sound played.
The speed of the generated code is set by the control currently labeled "5 wpm", for five words per minute.
morse_tree_extended

Here's a snap quiz: What is Morse code for the @ sign? Download morse_tree to check your answer.
- Category:
- Algorithms,
- Fun,
- Graphics,
- History
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.