Quaternions are generalizations of the complex numbers that have found applications in computer graphics and many other fields.... 続きを読む >>

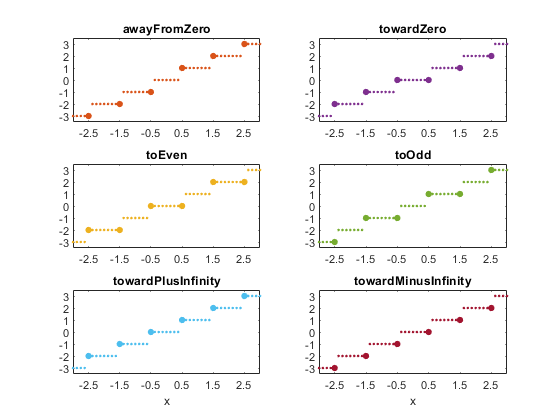
In February and March I published three blog posts about an enhancement request for MATLAB concerning tie breakers with the round function, including the ability to round ties to even. Round One, Round Two and Round Three. Since then, a group of us at MathWorks, organized by my colleague (and academic great-great-grand-descendant) Heiko Weichelt, have been considering the request. We had a virtual design review recently. This post describes a prototype incorporating the features that were discussed at that review.... 続きを読む >>

Nick Higham's Numerical Linear Algebra group at the University of Manchester is hosting a conference celebrating Jack Dongarra's 70th birthday July 7 and 8. I am giving a talk, virtually, on July 7. I plan to reminisce about how I did computing in the days before everybody had their own computer in their lap. Here are the slides for the talk, some notes, and some links to this blog for more details.... 続きを読む >>

I am giving a five-minute talk today, May 26, at the virtual seminar on Complexity of Matrix Computations. Here are my slides. Two new MATLAB functions, tred and imtql, instrumented to count flops, are available in symeig.m.... 続きを読む >>

Computing Eigenvalues of Symmetric MatricesSee revision.Get the MATLAB code (requires JavaScript) Published with MATLAB®... 続きを読む >>

The Bucky Ball provides an elegant example of a graph, the connectivity of the Buckminster Fuller geodesic dome.We are also demonstrating publishing this blog with the Live Editor. There is a button... 続きを読む >>

This is about linear systems with fewer equations than variables; A*x = b where the m -by- n matrix A has fewer rows that columns, so m < n . I have always called such systems wide or fat, but this is not respectful. So I consulted the Merriam-Webster Thesaurus and found commodious.... 続きを読む >>

What do the years 2018, 2029 and 2040 have in common? They are the only years in the 21st century when Easter Sunday occurs on April Fools Day.... 続きを読む >>

A news story released yesterday, March 31,by c|net has the headline... 続きを読む >>

What do Mount St. Helens and the rank of a matrix have in common? The answer is the MATLAB function peaks. Let me explain. Please bear with me -- it's a long story.... 続きを読む >>