Loren Shureが MATLAB で初めてのページ単位処理の行列関数を紹介する記事を投稿したのが 2021 年。ページ単位処理の行列乗算であるpagemtimes、転置 pagetranspose、そして複素共役転置の pagectranspose が紹介され、これらはすべて MATLAB R2020b で追加されました。

以下の図で視覚化してみます。各 3D 配列は、一連の行列（またはページ）と見なされます。

例えば A と B は、それぞれ 3×3 サイズの行列が3D方向に100,000 個あると想像してください。これらの各ペアを乗算して 3D 配列 C を形成したいとします。こちらがループを使用した古い方法です。

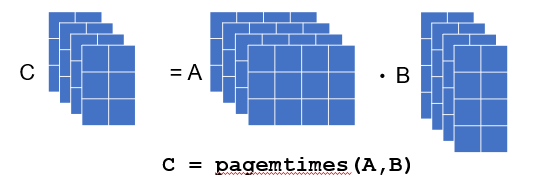
そしてを pagemtimes 使うと

処理時間はずっと速くなります。

結構なスピードアップですね。実際、この例は後ほど説明する理由から、 pagemtimes に期待できる最大のスピードアップを示すために選んでいます。

ページ単位処理の行列関数のアイデアは、人気があり、役立つことがわかりました！MathWorks では、私たちの製品全体とユーザーコミュニティで使用されているのを見かけましたし、さらにいくつかの変種について要望がありました。ページ単位処理の行列乗算は素晴らしいスタートで、ページ単位処理の SVD、バックスラッシュ、eig なども欲しいと思っていました。MathWorks の開発チームはそれらを実現しました！

それでは、R2024a 時点でのページ単位の行列関数の現状をもう少し詳しく見てみましょう。

以下が MATLAB にあるページ単位の行列関数のリストと、それらが導入された時期です。

自然な疑問です。「たくさんのページ関数を持つ代わりに、必要な関数を引数として受け取る pagefun という1つの関数を実装するのはどうか」実際、MATLAB には分散配列や GPU 配列で動作するParallel Computing Toolbox 内にそのような関数があります。

私たちもそれを検討しましたが、その理由の1つにオプション処理がありました。一部のオプションは特定の関数にのみ適用される可能性があります。オプションのドキュメントは長くなり、そのほとんどが誰かが行いたいことに関連しないものになります。もう 1 つの理由はパフォーマンスです。

ページ単位の行列関数に関する元のブログ投稿の多くは、ループを使用するよりもどれだけ速くなるかに焦点を当てていました。上記の例では、特定の場合にこのスピードアップが顕著であることを示しました。では、このスピードアップはどこから来るのでしょうか？

引数チェック：最初の最適化はありふれたものです。引数チェックです。ページ単位処理の場合、一度だけ行う必要がありますが、100,000 ページをループする場合は、100,000 回引数チェックを行うことになります。大きな行列の場合、このオーバーヘッドは無視できますが、非常に小さな行列を数千扱う場合、引数をチェックする時間は無視できなくなります。

より多くの並列性：スピードアップの 2 つ目の理由は並列性です。内部の for ループを全てのページで並列に実行することを選択できます。ここで事情はもう少し複雑になります。MATLAB の線形代数関数のほとんどは既に並列で実行されています。大きな行列を 2 つ乗算しながら CPU の負荷を監視すると、これが実際に行われているのを見ることができます。これにより、我々は決断を下す必要があります。基本となる BLAS/LAPACK ルーチンをマルチスレッドで実行させ、ページをまたいだループをスレッド化しないか、またはBLAS/LAPACK をシングルスレッドで実行し、外側のループをスレッド化するかを決める必要があります。

非常に小さい行列の場合、この決断は簡単です。非常に小さい行列を 2 つ乗算する場合、並列性から得られる利益はほとんどないでしょう。しかし、100,000 ペアがある場合、並列化への道は明らかです。

小さい行列の数学的トリック：ページ単位の関数を使用した主なスピードアップが多くの小さな行列で起こるため、そのような小さな行列（例えば 3×3）のパフォーマンスに焦点を当てるようにしました。これは、様々な数学的トリックを使用しています。これらのスピードアップは、inv や mldivide などの標準的な MATLAB 関数にも適用されました。例えば、mldivide のドキュメントを見ると、これがわかります。

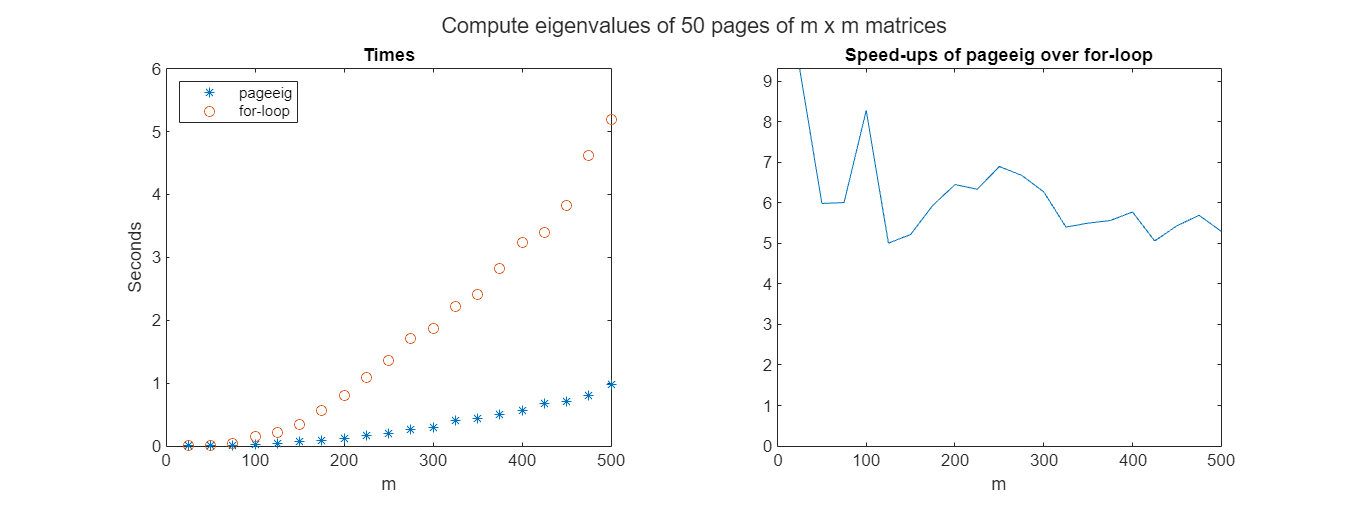
これら全ての結果として、膨大な数の小さな行列演算で特に処理時間が速くなります。しかしながら、それを踏まえた上で、paigeeig のデモが示すように、3D 方向の数が少ない より大きな行列サイズにおいても、依然として有用なスピードアップが見られます。

私は仕事の一環として、世界中の MATLAB ユーザーと協力してコードの実行速度を上げることがありますが、ページ単位処理の関数が導入されて以来何度か使用してきました。ユーザーのコードについては通常、お話しすることはできないので、MathWorks 内でどこで使用されているか尋ねてみました。答えは「Almost everywhere!」でした。

例えば、様々な Toolbox にまたがる100以上の関数が pagemtimes を使用していることがわかりました。例えば・・5G Toolbox, Aerospace Toolbox, Antenna Toolbox, Audio Toolbox, Communications Toolbox, System Identification Toolbox, Image Processing Toolbox, Lidar Toolbox, Medical Imaging Toolbox, Navigation Toolbox, Deep Learning Toolbox, Partial Differential Equation Toolbox, Phased Array System Toolbox, Radar Toolbox, RF Toolbox, Text Analytics Toolbox, Computer Vision Toolbox, WLAN Toolbox、そして MATLAB Support Package for Quantum Computing で使用されています。ページ単位処理の行列関数の概念が技術計算の多様な分野で役立っていることを示しています。

開発チームの一人が、現代の通信システムでは OFDM と呼ばれる技術が使用されており、データが隣接する一連の周波数で並列に空中に送信されると教えてくれました。各周波数では、受信機がチャネルからの歪みを解除しようとする等化処理があり、これを行うためには、各周波数で最小二乗問題（Ax = bまたはAx + n = b、ここでnは加法ガウスノイズを表す）を解きます。

これらの最小二乗問題は、関連する全ての周波数で pagesvd のようなルーチンを使用して並列に解くことができます。これにより、ofdmEqualize（Communications Toolbox）、nrEqualizeMMSE（5G Toolbox）、wlanHEEqualize（WLAN Toolbox）などの Toolbox 関数の大幅なスピードアップが実現しました。このスピードアップは、NR PDSCHスループット などの人気のあるデモコードで顕著なスピードアップにつながりました。

ページ単位の行列関数は、多くの MathWorkers の道具として非常に役立つ追加となりました。皆さんのコードの中でどこで適用できそうか検討されることをお勧めします。また、皆さんのコードで役立ったという場合は、ぜひコメントで教えてください。

ご存知の通り、全ては pagemtimes から始まりました。そこから、MATLAB の社内外のユーザーから他の関数に対する要望が寄せられ、それらを着実に追加してきました。実際に関数を実装する主な動機は、その利用用途です。特定のアプリケーション領域で使用できるページ単位処理の関数は、「foo は行列関数なので、pagefoo を実装してみては？」よりも優先されます。
もしこの記事があなたの興味を引き、まだ実装されていないページ単位処理の関数から恩恵を受けることができるアプリケーションをご存じの場合は、ぜひ詳細をお知らせください。