Optimizing a Structural Design
Today you'll see a new demonstration of applying optimization techniques. Today's guest is Takafumi Ohbiraki. This demonstration was part of the contents of the MATLAB EXPO which was held in Tokyo last year (2016).
Contents
- Design of an umbrella hook
- FEM model (Using Partial Differential Equation (PDE) Toolbox)
- Process of Optimization
- Design of Experiments (DOE) (Taguchi design)
- Calculation with setting parameters for L18
- Factor Effect Chart
- S/N ratio
- Output
- Optimization using patternsearch solver
- Optimization using ga solver
- Multi-objective optimization using the gamultiobj solver
- Conclusion
Optimization is a universal topic in both engineering and data science. It is a technology with high needs. Speaking of optimization in engineering, parameter estimation is often performed on a model showing a physical phenomenon.
Generally, when expressing a physical phenomenon by a model, MATLAB has functions of ordinary differential equations and partial differential equations,and performs simulation. For example, since the problem of heat conduction can be represented by parabolic partial differential equations on the second floor, it is possible to simulate with the function pdepe.
In reality, it is often difficult to convert a physical phenomenon into a closed-form mathematical formula. So it is common to utilize a modeling tool to convert the problem into a mathematical model for analysis.
At this time, we will introduce how to optimize the design by using Partial Differential Equation Toolbox and Optimization Toolbox with an example of structural analysis.
Design of an umbrella hook
A cool umbrella hook is always seen in Japanese public restrooms.

As a designer of an umbrella hook, we will consider how to reduce the cost by reducing the materials used for an umbrella hook. However, in order to keep the functionality of the umbrella hook, it is necessary to for the hook not to bend.
First, we define the design specifications. We consider opening an elliptical cavity in the member. The material (A or B) of the member, the coordinates (X, Y) of the ellipse, the radius of the ellipse (RX, RY), and the rotation angle of the ellipse (theta) are design parameters. The number of parameters is seven.
We will set the downward load on the tightening portion at the upper right and the fixed end at the left end. We perform an optimization with the aim of minimizing the displacement amount of the lower right point.

All parameters have the following constraints.

FEM model (Using Partial Differential Equation (PDE) Toolbox)
We create a function pdesample to actually simulate with parameters using Partial Differential Equation Toolbox (PDE Toolbox).
input: [material x-position y-position x-radius y-radius stick theta] output : strain
in = [1 5,2,1.5,1.0,0.3,0];
lh = pdesample
out = lh{1}(in)
lh =
5×1 cell array
@pdesample_input
@pdesample_input_doe_sn
@myobjfun
@myobjfun2
@mynoncon
out =
0.40131

This is the initial condition.
Output is about 0.4013. We do not understand whether this result is good or bad. We will seek a good answer using optimization techniques.
Process of Optimization
To actually perform the optimization calculation, if there are too many parameters, it takes time to reach the optimum value. This time, we will utilize a two-step optimization method that is often used in quality engineering. According to the two-step design method, first, make efforts to reduce the number of variables to be optimized by utilizing the experimental design method. In this method, we adopt the Taguchi design. The orthogonal table is uploaded to the File Exchange. In variable selection, we paid attention to the signal to noise ratio (S/N) ratio and the nominal-is-best response. In the second step, we use optimization algorithms to find good parameters.

Design of Experiments (DOE) (Taguchi design)
We will exploit which parameters should be reduced by utilizing the orthogonal array famous from the Taguchi design. In the orthogonal array of Taguchi design, there are 2 factors, 3 factors, and mixed orthogonal tables. We chose the famous L18 model for mixing both 2 factors and 3 factors.
L18 model : 18 experiments to make the combination of 8 variables efficient; one variable (material) is 2 levels , seven variables are 3 levels. The variable design created by my helper function orthogonalarray is a MATLAB table.
design = orthogonalarray('L18','Bounds',[1 2;2.0 8.0;1.0 3.0;0.5 1.9;0.2 0.9;0.1 0.3;-pi/12 pi/12;0 0],... 'VariableNames',{'material','x','y','rx','ry','dh','theta','xxx'})
design =
18×8 table
material x y rx ry dh theta xxx
________ _ _ ___ ____ ___ _______ ___
1 2 1 0.5 0.2 0.1 -0.2618 0
1 2 2 1.2 0.55 0.2 0 0
1 2 3 1.9 0.9 0.3 0.2618 0
1 5 1 0.5 0.55 0.2 0.2618 0
1 5 2 1.2 0.9 0.3 -0.2618 0
1 5 3 1.9 0.2 0.1 0 0
1 8 1 1.2 0.2 0.3 0 0
1 8 2 1.9 0.55 0.1 0.2618 0
1 8 3 0.5 0.9 0.2 -0.2618 0
2 2 1 1.9 0.9 0.2 0 0
2 2 2 0.5 0.2 0.3 0.2618 0
2 2 3 1.2 0.55 0.1 -0.2618 0
2 5 1 1.2 0.9 0.1 0.2618 0
2 5 2 1.9 0.2 0.2 -0.2618 0
2 5 3 0.5 0.55 0.3 0 0
2 8 1 1.9 0.55 0.3 -0.2618 0
2 8 2 0.5 0.9 0.1 0 0
2 8 3 1.2 0.2 0.2 0.2618 0
Calculation with setting parameters for L18
At experimental points, we calculate the outputs (strain) and S/N ratios.
output = zeros(18,1); sn = zeros(18,1); for i = 1:18 output(i,1) = lh{1}(table2array(design(i,1:8))); sn(i,1) = lh{2}(table2array(design(i,1:8))); end results = [design table(output,sn)]
results =
18×10 table
material x y rx ry dh theta xxx output sn
________ _ _ ___ ____ ___ _______ ___ _______ ______
1 2 1 0.5 0.2 0.1 -0.2618 0 0.346 108.16
1 2 2 1.2 0.55 0.2 0 0 0.36042 88.027
1 2 3 1.9 0.9 0.3 0.2618 0 0.42694 57.447
1 5 1 0.5 0.55 0.2 0.2618 0 0.35443 88.063
1 5 2 1.2 0.9 0.3 -0.2618 0 0.37875 78.837
1 5 3 1.9 0.2 0.1 0 0 0.36595 84.527
1 8 1 1.2 0.2 0.3 0 0 0.33836 121.1
1 8 2 1.9 0.55 0.1 0.2618 0 0.38466 59.585
1 8 3 0.5 0.9 0.2 -0.2618 0 0.34978 96.122
2 2 1 1.9 0.9 0.2 0 0 1.8659 32.802
2 2 2 0.5 0.2 0.3 0.2618 0 0.92894 132.08
2 2 3 1.2 0.55 0.1 -0.2618 0 0.97881 90.175
2 5 1 1.2 0.9 0.1 0.2618 0 1.2566 41.031
2 5 2 1.9 0.2 0.2 -0.2618 0 1.0356 78.99
2 5 3 0.5 0.55 0.3 0 0 0.94161 113
2 8 1 1.9 0.55 0.3 -0.2618 0 1.019 59.27
2 8 2 0.5 0.9 0.1 0 0 0.95126 106.67
2 8 3 1.2 0.2 0.2 0.2618 0 0.95404 88.904

Factor Effect Chart
The factor effect diagram is a graph expressing the effect of each factor, with the horizontal axis representing the level of the factor and the vertical axis representing the S / N ratio and the characteristic value. From this graph, find the condition with high S / N ratio and select the one with better characteristics.
factoreffectchart is my helper function.
S/N ratio
According to this chart, the S/N ratio is very good at both the 1st level of the 4th and 5th parameters (or variables).
The 4th variable is the x radius and the 5th variables is the y radius.
d = orthogonalarray('L18'); Osn = factoreffectchart(d,results.sn) % S/N
Osn =
86.873 82.546 NaN
84.781 80.741 88.608
75.07 90.698 88.362
107.35 84.679 62.103
102.29 83.019 68.818
81.69 78.818 93.621
85.258 91.02 77.851
80.213 83.509 90.407

Output
To minimize the strain, the 1st level of the 1st variable is good.
The 1st variable is material.
We succeed at reducing the parameters from 7 variables to 4.
O = factoreffectchart(d,results.output) % Output
O =
0.36726 1.1035 NaN
0.81783 0.72215 0.66618
0.86336 0.67327 0.66952
0.64534 0.71116 0.84967
0.66149 0.67315 0.87153
0.71387 0.82003 0.67226
0.68465 0.80391 0.7176
0.81182 0.71343 0.6809

Optimization using patternsearch solver
We will optimize 4 parameters using the patternsearch solver.
First of all, we are going to optimize the location of the hole that minimizes strain.
The objective function is the code from 192 to 197 lines in "pdesample.m".
dbtype pdesample 193:197 close all
193 function out = myobjfun(in) 194 195 out = pdesample_input([1 in(1) in(2) 0.5 0.2 in(3) in(4)]); 196 197 end
opt = optimoptions('patternsearch'); opt.MeshTolerance = 0.001; opt.FunctionTolerance = 0.00001; opt.MaxIterations = 500; opt.TimeLimit = 10*60; opt.UseParallel = true; opt.Display = 'iter'; [x,obj] = patternsearch(lh{3}, [7,3,0.2,0],[],[],[],[],[2.0,0.3,0.1,-pi/4],[9.5,4.5,0.3,pi/4],lh{5},opt)
Max
Iter Func-count f(x) Constraint MeshSize Method
0 1 0.338279 0 1
1 6 0.33769 0 0.009772 Update multipliers
2 329 0.334631 0 0.000955 Update multipliers
Optimization terminated: mesh size less than options.MeshTolerance
and constraint violation is less than options.ConstraintTolerance.
x =
9.3125 2.9688 0.14141 0.25
obj =
0.33463

Optimization using ga solver
We will also optimize 4 parameters using the ga> solver.
gaoptions = gaoptimset(@ga); gaoptions.CrossoverFcn = @crossoverintermediate; gaoptions.MutationFcn = @mutationadaptfeasible; gaoptions.CrossoverFraction = 0.5; gaoptions.TolFun = 0.00001; gaoptions.PopulationSize = 20; % population size gaoptions.InitialPopulation = [7,3,0.2,0]; % initial population gaoptions.Generations = 500; % gaoptions.TimeLimit = 10*60; gaoptions.UseParallel = true; gaoptions.Display = 'iter'; [x,fval] = ga(lh{3},4,[],[],[],[],[2.0,0.3,0.1,-pi/4],[9.5,4.5,0.3,pi/4],lh{5},gaoptions)
Best Max Stall
Generation Func-count f(x) Constraint Generations
1 1078 0.33505 0 0
2 1598 0.334569 0.0008296 0
Optimization terminated: average change in the fitness value less than options.FunctionTolerance
and constraint violation is less than options.ConstraintTolerance.
x =
9.3345 3.1148 0.19511 0.36912
fval =
0.33457
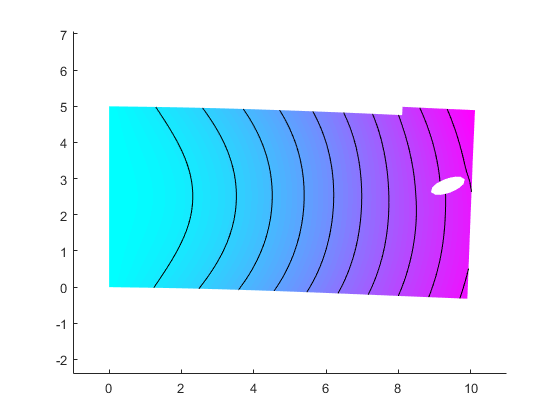
The values of the output by both the patternsearch and ga solvers are reduced from the inital conditions. Both results give especially similiar results for the x,y positions. We conclude that both results are good. However, the area of hole is the smallest possible because of considering the S/N ratio. In order to lighten the weight, we will enlarge the area of hole.
Multi-objective optimization using the gamultiobj solver
We would like to optimize both the size and location of the hole in order to minmize the strain and lighten the weight.
In the previous case, radius x and y are the minimum values. In order to increase the size of the hole, we will use a multi-objective optimization gamultiobj solver.
The relationship between the value of strain and the area of hole is inverse proportional and there is a trade-off.
The objective function is the code from 200 to 205 lines in "pdesample.m".
dbtype pdesample 200:205
200 function out = myobjfun2(in) 201 202 out(1) = pdesample_input([1 in 0.2 0*pi/12]); 203 out(2) = -pi*in(3)*in(4); 204 205 end
mulgaoptions = gaoptimset(@gamultiobj);
mulgaoptions.CrossoverFraction = 0.5;
mulgaoptions.TolFun = 0.001;
mulgaoptions.PopulationSize = 100;
mulgaoptions.Generations = 3000;
mulgaoptions.InitialPopulation = [7 2.5 0.5 0.5];
mulgaoptions.UseParallel = false;
mulgaoptions.TimeLimit = 20*60;
[x,fval,exitflag,output] = gamultiobj(lh{4},4,[1 0 1 0;0 1 0 1;-1 0 1 0; 0 -1 0 1],[9.9;4.9;-0.2;-0.2],[],[],[2.0,0.3,0.2,0.2],[9.6,4.5,3,2.6],mulgaoptions);
Optimization terminated: time limit exceeded.

Here is the biggest hole.
lh{4}(x(1,:))
ans =
0.33632 -0.62854

In this next plot, we show the pareto frontier which is popular for design engineering. There you can see the trade-off between area and strain for making design decisions.
scatter(fval(:,1),50.4 + fval(:,2),'m') set(gca,'FontSize',16,'FontName','Meiryo UI') xlabel('strain');ylabel('area');title('pareto frontier')

Pareto frontier results.
T1 = array2table([fval(:,1) 50.4+fval(:,2) x],'VariableNames',{'Strain','Area','x','y','rx','ry'})
T1 =
35×6 table
Strain Area x y rx ry
_______ ______ ______ _______ _______ _______
0.33632 49.771 8.4674 0.83566 0.54447 0.36746
2.9137 29.829 6.1874 2.4294 2.9804 2.197
0.8458 36.385 6.1587 2.0938 2.7957 1.5957
3.9636 29.123 6.1812 2.593 2.9923 2.2634
1.553 32.151 5.883 2.3126 2.9526 1.9674
0.83451 37.023 6.7695 2.1714 2.4951 1.7065
0.42155 44.452 7.107 2.1224 1.3364 1.4167
1.2357 33.732 6.0206 2.5458 2.879 1.8429
0.93663 35.477 6.1315 2.3105 2.9743 1.5971
0.75125 37.875 6.7413 2.0409 2.5471 1.5653
1.0758 34.69 6.385 2.4479 2.8222 1.7719
3.077 29.714 6.1778 2.4877 2.9777 2.2113
2.8688 29.875 6.022 2.4611 2.9817 2.1911
0.39498 45.353 7.3136 1.8261 1.4593 1.1008
1.1526 34.152 6.2626 2.1237 2.9141 1.7747
0.35257 47.25 8.2497 1.2095 1.0588 0.94702
3.4396 29.299 6.3585 2.4648 3 2.2389
1.4782 32.434 6.1279 2.4721 2.9814 1.9181
2.1484 30.683 5.9299 2.4064 2.9995 2.0924
0.50403 41.862 7.0168 2.0862 1.8298 1.4853
2.3041 30.529 5.9573 2.4324 2.9834 2.1201
1.6972 31.718 5.9601 2.4295 2.9809 1.995
3.2141 29.467 6.1923 2.4677 3 2.221
0.34045 48.795 8.1318 1.0284 0.8714 0.58627
1.0626 35.115 6.6304 2.3413 2.6315 1.8489
1.3309 33.168 6.023 2.5945 2.9801 1.8405
0.38738 45.534 7.4165 1.5702 1.5472 1.0012
1.4303 32.719 5.9897 2.279 2.8842 1.9514
0.55291 40.816 5.8008 1.8469 2.672 1.1418
1.8278 31.425 5.9551 2.491 2.9899 2.0201
0.3506 48.091 8.7273 1.5772 0.62704 1.172
1.9699 31.13 6.0712 2.4664 2.98 2.0583
3.7843 29.133 6.0624 2.4919 2.9961 2.2595
2.7137 30.065 6.191 2.4831 2.9761 2.1749
3.6181 29.252 5.7451 2.5008 2.9962 2.2467
Conclusion
We showed how to use FEM tools and Optimization Toolbox to perform structural design. What can you shape with these tools? Let us know your thoughts here.
- Category:
- Fun,
- Optimization,
- Parallel,
- PDE









Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.