Fill Image NaN Values with Local Average
Recently we had a customer ask how to fill in NaN values in an image with a neighborhood local mean. My friend, colleague, and occasional blogger, Brett Shoelson, joins me today to show you several viable techniques.
Contents
Create data
Let's create an image and artificially create some holes with NaNs. It's a image of type uint8, and can't represent NaN values so we are going to convert to floating point.
img = imread('rice.png'); whos img
Name Size Bytes Class Attributes img 256x256 65536 uint8
thisIsWhatHappens = uint8(NaN)
thisIsWhatHappens = uint8 0
Convert image from uint8 to single.
singleImg = im2single(img); tlo = tiledlayout(2,2, 'TileSpacing', 'compact', 'Padding', 'none'); nexttile(tlo); imshow(singleImg)

Add some NaN values. Single rice grains are smaller than 270 pixels, so we are choosing to introduce NaNs in areas larger than a typical grain. First we threshold the image to segment the grains of rice. And we discard blobs smaller than 270 pixels. This gives us a mask of large or contiguous rice grains. We replace these areas in the original image with NaNs. You can see that in the 3rd image.
nanMask = imbinarize(singleImg,"adaptive");
nanMask = bwareaopen(nanMask, 270);
nexttile(tlo)
imshow(nanMask)
singleImgNaN = singleImg;
singleImgNaN(nanMask) = NaN;
nexttile(tlo)
imshow(singleImgNaN)

Let's now consider several approaches for filling in these NaN regions.
Use regionfill to Replace NaNs - Solution 1
regionfill provides an the "out-of-the-box," documented approach to region filling. It works well, and is fast. It fills regions in images using inward interpolation--in this case, replacing the NaNs with a smooth representation of local background values. If you're interested in the algorithm, visit the documentation page. This is your go-to algorithm for most region-filling needs.
imgrf = regionfill(img, nanMask); nexttile(tlo) imshow(imgrf)
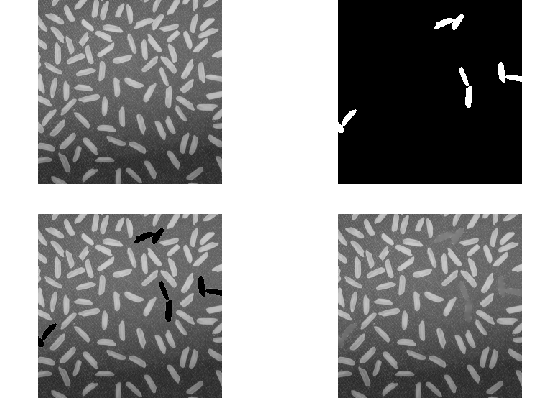
This works great, but is not necessarily what the customer asked for.
Replace NaNs with Local Average - Solution 2
Let's try something else next. Let's first define what we mean by "neighboring pixels".
If we have a single pixel, we can define its neighbors as "4-connected," meaning the pixels North, East, South, and West are neighbors, or we can define neighbors as "8-connected," in which case we include NE, SE, SW, and NW in addition. We can represent these as offsets relative to a pixel position in the image.
One caution: we need to be careful to not step beyond the edges of the image, so we will pad the image with a 1-pixel border of zeros. (The functions in the <https://www.mathworks.com/products/image.html Image Processing Toolbox > take care of such things for you, when necessary.)
Add a single-pixel black frame around the perimeter of the image:
paddedImg = padarray(singleImgNaN, [1 1], 0, 'both');
Create 4-connected and 8-connected offsets.
[m, n] = size(singleImg); neighbors4 = [-1, 1, m, -m]; neighbors8 = [neighbors4, -m-1, -m+1, m-1, m+1];
We don't necessarily want to change the output size of the image. To accommodate this, we can treat the positions in the original image separately from the padded image.
Let's find NaNs first.
originalNaNPos = find(isnan(singleImgNaN)); paddedImageNaNs = find(isnan(paddedImg));
We're going to overwrite individual pixels in the output image so we are making a copy we can alter.
imglocav = singleImgNaN;
We can create and use some anonymous functions to compute the means using the 2 different neighborhood definitions, ignoring NaNs.
f4 = @(ind) mean(paddedImg(ind + neighbors4),"omitnan"); f8 = @(ind) mean(paddedImg(ind + neighbors8),"omitnan");
Let's show what this looks like for 4-connected neighbors. We find the positions of the NaNs in the padded image, and compute the neighbor means for each of these. We then take this computed values and replace the corresponding location in the original image with these.
for ii = 1:numel(paddedImageNaNs) imglocav(originalNaNPos(ii)) = f4(paddedImageNaNs(ii)); end imshow(imglocav)
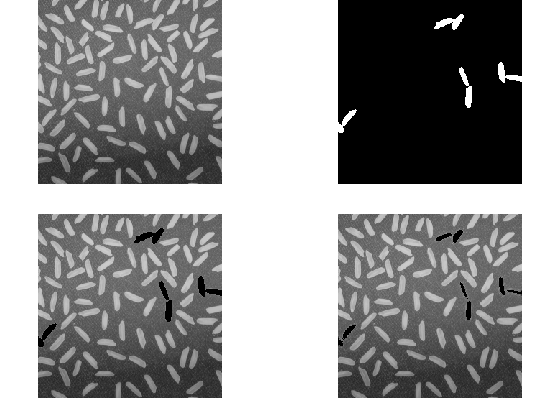
Hmmm
Well, we see the first problem with this approach: any NaN pixel that is surrounded entirely by NaN neighbors--will be replaced with a NaN!
whyNaN = mean(nan(4, 1), "omitnan")
whyNaN = NaN
So while we've shrunk the NaN-holes, we haven't entirely removed them. (Notice that when we zoom in and use impixelinfo we can see the values of the pixels we're talking about.)

So what to do?
Let's iterate! Now let's consider what happens if we iterate until there are no more NaNs.
Let's reset our image first.
imglocav = singleImgNaN;
Now iterate
while nnz(isnan(imglocav)) > 0 originalNaNPos = find(isnan(imglocav)); for ii = 1:numel(originalNaNPos) imglocav(originalNaNPos(ii)) = f4(paddedImageNaNs(ii)); end end imshow(imglocav)
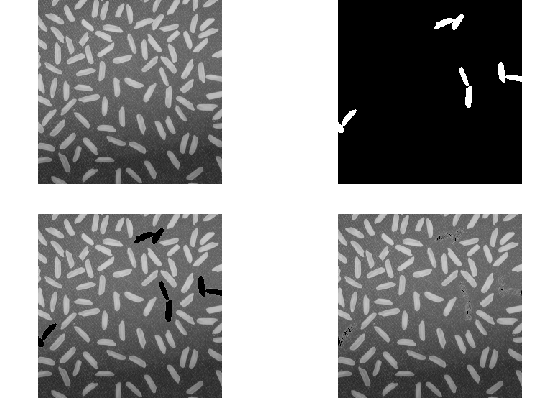
We think this is what the customer was asking for, but now we see a potential second problem: the NaN pixels that were entirely surrounded by NaNs in their four- or eight-connectedness, have been replaced with zeros.
The computer did what we asked, but not necessarily what we wanted!
Use Region Labeling to Fill - Solution 3
We are going to take advantage of the nanMask we computed earlier. We find the outlines, and label distinct connected areas. Next we loop over each area and fill each one with the mean of its perimeter values. No iteration is necessary, but we will end up with flat regions of uniform intensity.
edgeMask = edge(nanMask); bwl = bwlabel(edgeMask); bwl2 = bwlabel(nanMask); imX = singleImgNaN; for ii = 1:max(bwl(:)) thisEdgeMean = mean(imX(bwl == ii), "omitnan"); imX(bwl2 == ii) = thisEdgeMean; end imshow(imX)

Others?
What other ways do you think about this problem? We know there are a lot of different ways. Let us know here.
- 类别:
- Image Processing









评论
要发表评论,请点击 此处 登录到您的 MathWorks 帐户或创建一个新帐户。