Why do we need Stiff ODE Solvers?
I hope you have noticed the new MATLAB Central blog: Cleve's Corner. Cleve once said "stiffness is an efficiency issue." Let's explore this from a Simulink point of view by revisiting an article by Cleve in MATLAB News and Notes, May 2003: Stiff Differential Equations.
Example Problem
If you search the web for stiff systems or stiff solvers, you will very likely encounter a simple model of flame propagation used by Larry Shampine, one of the authors of the MATLAB ODE suite.
As described by Cleve:
When you light a match, the ball of flame grows rapidly until it reaches a critical size. Then it remains at that size because the amount of oxygen being consumed by the combustion in the interior of the ball balances the amount available through the surface.The simple model is:
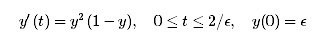
Where y is the radius of the flame ball.
Implemented in Simulink, this equation look like that:

When simulating this system using an initial value of 1e-4, all Simulink variable-step solver will give a result close to this:
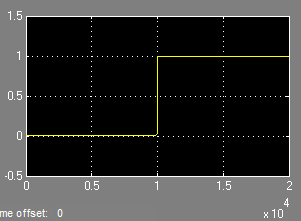
As you can see, the output is flat most of the time, but shows a very fast sudden transition. This is typical of stiff systems.
Analyzing Solvers Behaviors
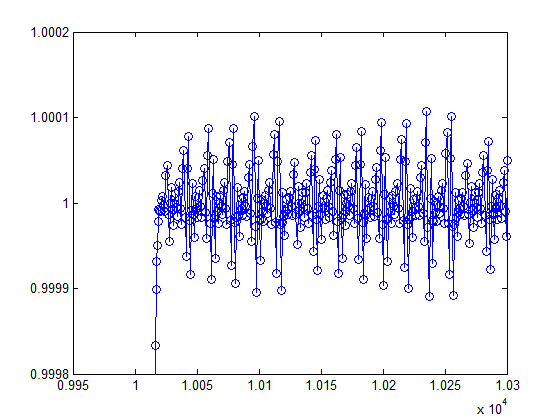
Let's compare the results between ode45 and ode23s. If we zoom on a small period of time after the transition at 10,000 seconds, we can observe that the results from ode45 shows oscillations:
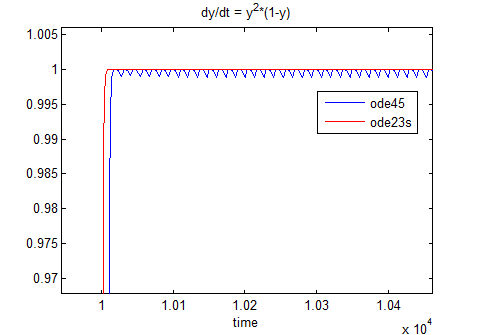
Those small oscillations force the ode45 solver to take very small steps. If we use the command I introduced in a previous post to compare the time steps taken by the 2 solvers, we can see the following:
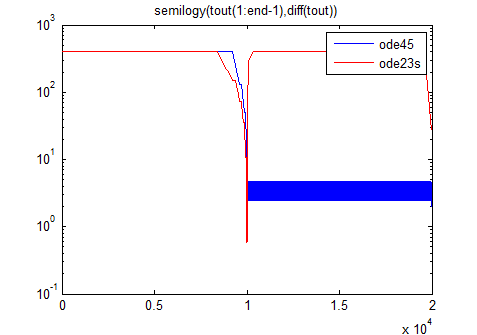
As you can see, ode45 is not able to recover after the fast transition and keeps taking very small steps. In this specific example, ode45 required 3046 steps to solve the problem, while ode23s required only 91 steps! Ode23s may do more computations per step, but it can take fewer steps than ode45.
Conclusion
To conclude, I would like to quote the analogy made by Cleve to illustrate the difference between stiff and non-stiff solvers:
Imagine you are returning from a hike in the mountains. You are in a narrow canyon with steep walls on either side. An explicit algorithm would sample the local gradient to find the descent direction. But following the gradient on either side of the trail will send you bouncing back and forth from wall to wall. You will eventually get home, but it will be long after dark before you arrive. An implicit algorithm would have you keep your eyes on the trail and anticipate where each step is taking you. It is well worth the extra concentration.
If you need more help selecting a solver, take a look at the documentation about how to pick a solver in Simulink.
Now it's your turn
Are stiff solvers important for your application? Let us know by leaving a comment here.








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.