Filtering fun
Today I want to take the test pattern I created last time and subject it to a variety of frequency-based filters.
In this post I'll be using a variety of frequency design and frequency-response visualization tools in MATLAB, Signal Processing Toolbox, and Image Processing Toolbox, including fir1, ftrans2, freqspace, fwind1, and freqz2. I won't be giving much explanation of these filter design techniques. Perhaps in the future I'll explore filter design here in more detail. For now, though, I really just want to have some fun with this test pattern.
[x,y] = meshgrid(-200:200); r = hypot(x,y); km = 0.8*pi; rm = 200; w = rm/10; term1 = sin( (km * r.^2) / (2 * rm) ); term2 = 0.5*tanh((rm - r)/w) + 0.5; g = (term1 .* term2 + 1) / 2; imshow(g, 'XData', [-.8 .8], 'YData', [-.8 .8]) axis on xlabel('Normalized frequency'), ylabel('Normalized frequency') title('Test pattern')
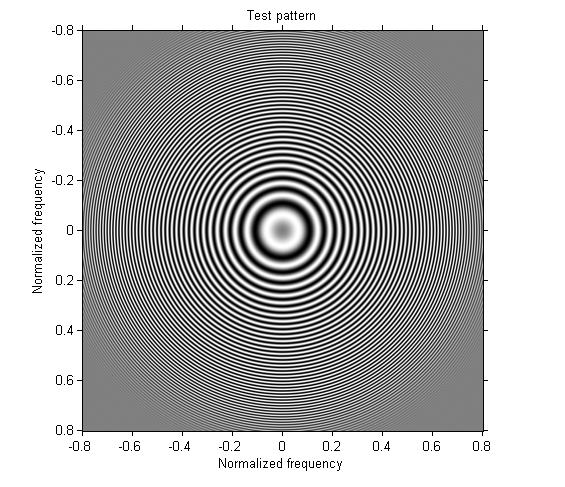
Example 1: Design a one-dimensional lowpass filter and apply it in both directions.
b = fir1(30,0.3); h = b' * b; g1 = imfilter(g, h); imshow(g1, 'XData', [-.8 .8], 'YData', [-.8 .8]) axis on xlabel('Normalized frequency'), ylabel('Normalized frequency')
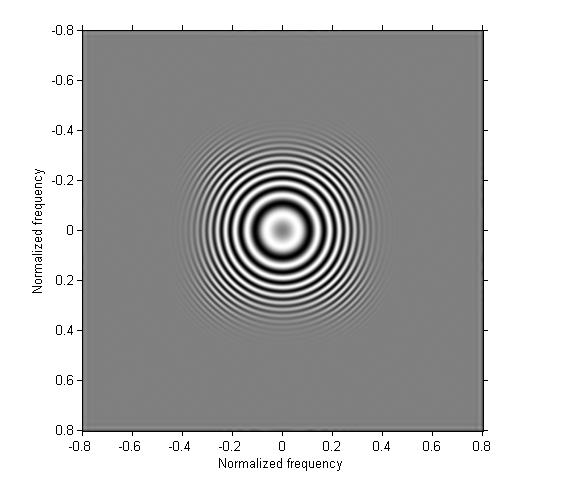
Example 2: Design a one-dimensional highpass filter and apply it in both directions.
b2 = fir1(30, 0.3, 'high'); h2 = b2' * b2; g2 = imfilter(g, h2); imshow(g2, [], 'XData', [-.8 .8], 'YData', [-.8 .8]) axis on xlabel('Normalized frequency'), ylabel('Normalized frequency')

Example 3: Design a one-dimensional bandpass filter and apply it on both directions.
b3 = fir1(30, [0.3 0.4]); h3 = b3' * b3; g3 = imfilter(g, h3); imshow(g3, [], 'XData', [-.8 .8], 'YData', [-.8 .8]) axis on xlabel('Normalized frequency'), ylabel('Normalized frequency')
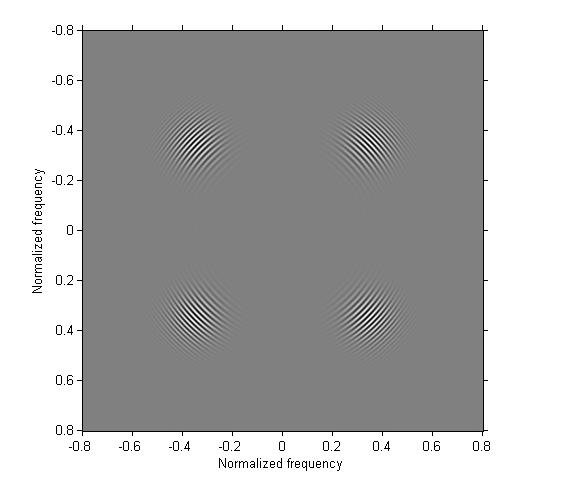
Example 4: Apply the one-dimensional bandpass filter from the previous step in only one direction.
g4 = imfilter(g, b3); imshow(g4, [], 'XData', [-.8 .8], 'YData', [-.8 .8]) axis on xlabel('Normalized frequency'), ylabel('Normalized frequency')

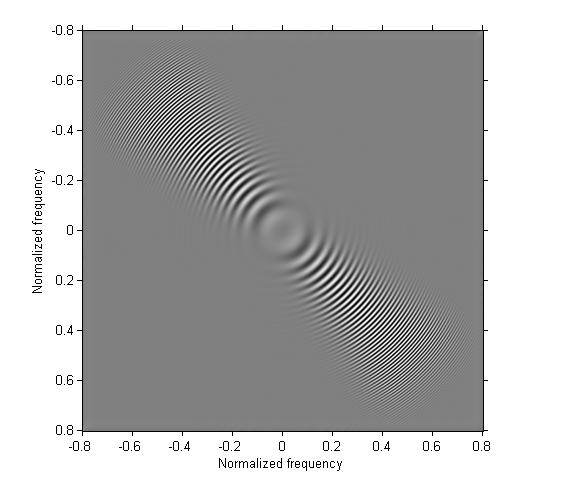
Example 5: Use ftrans2 to turn the one-dimensional bandpass filter from the previous example into a two-dimensional bandpass filter that is approximately circularly symmetric.
h5 = ftrans2(b3); g5 = imfilter(g, h5); imshow(g5, [], 'XData', [-.8 .8], 'YData', [-.8 .8]) axis on xlabel('Normalized frequency'), ylabel('Normalized frequency')

Example 6: Use fwind1 to design a two-dimensional filter that has a wedge-shaped frequency response.
[f1, f2] = freqspace(101, 'meshgrid'); theta = cart2pol(f1, f2); Hd = ((theta >= pi/6) & (theta < pi/3)) | ... ((theta >= -5*pi/6) & (theta < -2*pi/3)); mesh(f1, f2, double(Hd)) title('Ideal frequency response')

h6 = fwind1(Hd, hamming(31));
freqz2(h6)
title('Designed filter frequency response')
g6 = imfilter(g, h6); imshow(g6, [], 'XData', [-.8 .8], 'YData', [-.8 .8]) axis on xlabel('Normalized frequency'), ylabel('Normalized frequency')
Example 7: Compare the use of an averaging filter and a Gaussian filter. This example is inspired by Cris Luengo's comment from last week.
g7 = imfilter(g, fspecial('average', 9)); imshow(g7, [], 'XData', [-.8 .8], 'YData', [-.8 .8]) axis on xlabel('Normalized frequency'), ylabel('Normalized frequency') title('13-by-13 averaging filter')

You can see that some very high frequencies remain in the output. The Gaussian filter performs much better:
g9 = imfilter(g, fspecial('gaussian', 9, 2)); imshow(g9, [], 'XData', [-.8 .8], 'YData', [-.8 .8]) axis on xlabel('Normalized frequency'), ylabel('Normalized frequency') title('13-by-13 Gaussian filter')

OK, I'm going to give this test pattern a rest for now. Phew!
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.