Can One Hear the Shape of a Drum? Part 3, Transplantation.
This is the third part of a series of posts about Marc Kac's 1966 paper in the American Mathematical Monthly [1]. This part is devoted to the proof that the drums have the same eigenvalues.


 Now we transplant the finite difference eigenvector. The arrays A through G are the seven pieces. Each triangular piece of the transplanted eigenvector is the sum of three pieces of the original vector. The matrix transposes and rotations reproduce the dotted and dashed edges in Chapman's figure 2b.
Now we transplant the finite difference eigenvector. The arrays A through G are the seven pieces. Each triangular piece of the transplanted eigenvector is the sum of three pieces of the original vector. The matrix transposes and rotations reproduce the dotted and dashed edges in Chapman's figure 2b.
 We can now limit w to the grid points and use the discrete Laplacian from drum2.
We can now limit w to the grid points and use the discrete Laplacian from drum2.
Contents
Transplantation
This is a portion of the story behind a process known as transplantation that proves the drums are isospectral. The deeper mathematical aspects are in papers by Chapman [2], Berard [3], [4], Gordon and Webb [5], Gordon, Webb and Wolpert [6], and the work they reference.Seven triangles.
Each drum is made up of seven isosceles right triangles. Any eigenvector on either drum can be constructed from triangular pieces of the corresponding eigenvector on the other drum. The same argument applies to the continuous eigenfunction of the partial differential operator, and to the discrete eigenvector of the finite difference operator with any grid size. Since all pairs of eigenfunctions or eigenvectors have the same eigenvalues, the drums are isospectral.% The drums. clear all drum1 = [0 0 2 2 3 2 1 1 0 0 1 3 2 2 1 1 0 0]; drum2 = [1 0 0 2 2 3 2 1 1 0 1 2 2 3 2 1 1 0]; vertices = {drum1,drum2}; % The triangles. Tx = zeros(7,4,2); Ty = zeros(7,4,2); Tx(:,:,1) = [0 0 1 0; 0 1 1 0; 0 1 1 0; 1 1 2 1; 1 2 2 1; 1 2 2 1; 2 3 2 2]; Ty(:,:,1) = [0 1 0 0; 1 1 0 1; 1 2 1 1; 1 2 1 1; 2 2 1 2; 2 3 2 2; 2 2 1 2]; Tx(:,:,2) = [1 0 1 1; 0 1 1 0; 0 0 1 0; 1 1 2 1; 1 2 2 1; 2 2 3 2; 2 2 3 2]; Ty(:,:,2) = [0 1 1 0; 1 2 1 1; 1 2 2 1; 1 2 1 1; 2 2 1 2; 1 2 2 1; 2 3 2 2];
The map.
Here is a roadmap for the transplantation. Let's go from drum1 to drum2, although we could just as easily go from drum2 to drum1. Three copies of an eigenvector are broken into triangular pieces, rotated and possibly transposed according to the following formulas. For example, B-A'+G means the B triangle is unaltered, the G triangle is rotated clockwise $90^\circ$ to fit on top of B, and the A triangle, regarded as a lower triangular matrix, is transposed to create an upper triangular matrix, and subtracted from B+rot90(G,-1). Using three pieces of the one eigenvector makes it possible for the difference operator to work properly across the interfaces. The boundary values add or cancel so that the mapped vector conforms to drum2. Since only one eigenvector is mapped, the same eigenvalue applies on the second drum, establishing isospectrality. Jon Chapman has a very helpful description of this process in terms of paper folding [2]. S = {'B-A''+G'; 'A+C+E'; 'B-C''+D'; 'D-A''+F'; 'E-B''-F'''; 'F-C''+G'; ...
'E-D''-G'''};
for d = 1:2
clf
set(gcf,'color','white')
axis([-0.1 3.1 -0.1 3.1])
axis square off
for t = 1:7
line(Tx(t,:,d),Ty(t,:,d),'color','black','linewidth',2);
if d == 1
txt = char('A'+t-1);
else
txt = S{t};
end
text(mean(Tx(t,1:3,d)),mean(Ty(t,1:3,d)),txt,'horiz','center')
end
snapnow
end


Transplant any eigenvector.
eignum = 1
eignum =
1
Finite differences.
% Grid size. ngrid = 64; h = 1/ngrid; [x,y] = meshgrid(0:h:3); inpoints = (7*ngrid-2)*(ngrid-1)/2; lambda = zeros(eignum,2); V = zeros(inpoints,eignum,2); % Use "eigs" to compute the eigenvalue and eigenvector for both drums. for d = 1:2 vs = vertices{d}; [in,on] = inpolygon(x,y,vs(1,:),vs(2,:)); in = xor(in,on); % Number the interior grid points. G = double(in); p = find(G); G(p) = (1:length(p))'; grid{d} = G; % The discrete Laplacian Delta{d} = delsq(G)/h^2; % Sparse matrix eigenvalues and vectors. [V(:,:,d),E] = eigs(Delta{d},eignum,0); lambda(:,d) = diag(E); end
Triangular pieces.
U is the pieces of the eigenvector on drum1. W will be the pieces of the transplanted eigenvector on drum2. U = zeros(ngrid+1,ngrid+1,7);
W = zeros(ngrid+1,ngrid+1,7);
d = 1;
G = grid{d};
p = find(G);
u = zeros(size(G));
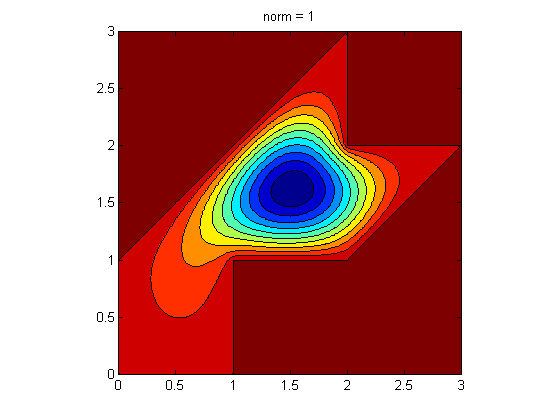
u(p) = V(:,1,1);
contourf(x,y,u)
title(['norm = ' num2str(norm(u(:)))])
axis square
for t = 1:7
in = inpolygon(x,y,Tx(t,:,d),Ty(t,:,d));
[i,j] = find(in);
U(:,:,t) = flipud(full(sparse(i-min(i)+1,j-min(j)+1,u(in))));
end
 Now we transplant the finite difference eigenvector. The arrays A through G are the seven pieces. Each triangular piece of the transplanted eigenvector is the sum of three pieces of the original vector. The matrix transposes and rotations reproduce the dotted and dashed edges in Chapman's figure 2b.
Now we transplant the finite difference eigenvector. The arrays A through G are the seven pieces. Each triangular piece of the transplanted eigenvector is the sum of three pieces of the original vector. The matrix transposes and rotations reproduce the dotted and dashed edges in Chapman's figure 2b.
A = U(:,:,1); B = U(:,:,2); C = U(:,:,3); D = U(:,:,4); E = U(:,:,5); F = U(:,:,6); G = U(:,:,7); % Here is all the work, in the next seven statements. a = B - A' + rot90(G,-1); b = rot90(A) + C + rot90(E,-1); c = rot90(B) - rot90(C',2) + rot90(D,-1); d = D - rot90(A',2) + rot90(F,-1); e = E - rot90(B',2) - rot90(F'); f = rot90(F,2) - rot90(C',2) + G; g = rot90(E,2) - rot90(D',2) - rot90(G'); W(:,:,1) = a; W(:,:,2) = b; W(:,:,3) = c; W(:,:,4) = d; W(:,:,5) = e; W(:,:,6) = f; W(:,:,7) = g; % Insert the triangular pieces back into the second drum. d = 2; G = grid{d}; p = find(G); w = zeros(size(G)); for t = 1:7 in = inpolygon(x,y,Tx(t,:,d),Ty(t,:,d)); [i,j] = find(in); v = zeros(length(i),1); for k = 1:length(i) v(k) = W(max(i)+1-i(k),j(k)-min(j)+1,t); end w(in) = v; end
Surprise.
I was very surprised when I found that the $l_2$ norm of most transplants is $\sqrt{2}$.norm_w = norm(w(:))
norm_w =
1.4142
The only exceptions are transplants of eigenvectors, like $v_9$, that are also eigenvectors of the embedded triangle. Then the norm is $3$ because the transplant mapping is just adding up three copies of the same vector.
Four checks for an eigenvector.
Check one, visual. This contour plot looks like an eigenvector of drum2.contourf(x,y,w) title(['norm = ' num2str(norm(w(:)))]) axis square
 We can now limit w to the grid points and use the discrete Laplacian from drum2.
We can now limit w to the grid points and use the discrete Laplacian from drum2.
w = w(p);
Delta = Delta{2};
Check two, compare the Rayleigh quotient to the expected eigenvalue. The error is tiny.
rho = (w'*Delta*w)./(w'*w) error = rho - lambda(1,2)
rho = 10.1584 error = 2.3626e-13Check three, apply the Laplacian. The residual is tiny.
residual = norm(Delta*w - rho*w)
residual = 1.3621e-11Check four, compare to the eigenvector computed by eigs. The error is tiny.
error = norm(w/norm_w - V(:,2))
error = 5.9747e-15
Where does $\sqrt2$ come from?
I have been working on this post off and on for weeks. All this time I have been baffled by the $\sqrt{2}$ that shows up as the norm of the transplanted eigenvector. It doesn't affect the eigenvector property because a scalar multiple of an eigenvector is still an eigenvector, but it sure was curious. I asked my friends who had written about the isospectral drums and they did not have any ready answers. On Monday of the week I am writing this post, I sent email to Jon Chapman at Oxford. In 1995 he had written about the paper folding interpretation of transplantation. I asked if he could explain the $\sqrt{2}$. On Tuesday he replied that he couldn't, but a few hours later he wrote again and told me about an amazing symbolic computation he had somehow been inspired to do in Mathematica. I can reproduce it here with the MATLAB Symbolic Toolbox.syms A B C D E F G norm_u_sq = A^2 + B^2 + C^2 + D^2 + E^2 + F^2 + G^2; norm_w_sq = (B-A+G)^2 + (A+C+E)^2 + (B-C+D)^2 + (D-A+F)^2 + ... (E-B-F)^2 + (F-C+G)^2 + (E-D-G)^2; z = simplify(2*norm_u_sq - norm_w_sq)
z = -(B - A - C + D - E + F + G)^2I use the letter z because the quantity turns out to be zero. The Laplacian of the vector in parentheses is zero and the vector vanishes on the boundary of a triangle, so the vector must be zero throughout the triangle. That is, unless the vector is an eigenvector of the triangle. Jon told me in a subsequent transatlantic phone call that he thinks of this as folding all seven triangles into one. The pieces of an eigenvector annihilate each other. This calculation and analysis implies $$ 2 ||u||^2 - ||w||^2 = 0 $$ Consequently $$ ||w|| = \sqrt{2} ||u|| $$ Thanks, Jon.
References
- Marc Kac, Can one hear the shape of a drum?, Amer. Math. Monthly 73 (1966), 1-23.
- S. J. Chapman, Drums that sound the same, Amer. Math. Monthly 102 (1995), 124-138.
- Pierre Berard, Transplantation et isospectralite, Math. Ann. 292 (1992), 547-559.
- Pierre Berard, Domaines plans isospectraux a la Gordon-Webb-Wolpert, Seminaire de Theorie spectrale et geometrie 10 (1991-92), 131-142.
- Carolyn Gordon and David Webb, You Can't Hear the Shape of a Drum, American Scientist 84 (1996), 46-55.
- Carolyn Gordon, David Webb, Scott Wolpert, One cannot hear the shape of a drum, Bull. Amer. Math. Soc. 27 (1992), 134-138.
- Wikipedia, Hearing the shape of a drum.
- Tobin Driscoll, Isospectral Drums.
- Tobin Driscoll, Eigenmodes of isospectral drums, SIAM Review 39 (1997), 1-17.
- Cleve Moler, Numerical Computing with MATLAB
- Cleve Moler, pdegui.m
- Category:
- Eigenvalues








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.