eigshow, week 3
An option in eigshow demonstrates SVD, the matrix singular value decomposition. The emphasis is on orthogonality.
Contents
The default matrix
This is the third posting about one of my favorite MATLAB programs, eigshow. The first two postings were about the 'eig' option for eigenvalues. This posting is about the 'svd' option for the singular value decomposition.
The default matrix, shown in the figure window title, is
format rat, format compact A = [1 3; 4 2]/4
A =
1/4 3/4
1 1/2

With the 'svd' option, you have two green vectors, x and y, that are perpendicular to each other and that have unit length. They remain perpendicular as you move x around the unit circle with the mouse, so they always form an orthonormal basis for two-dimensional space.
The two blue vectors, Ax and Ay, are images of x and y under the mapping induced by the matrix A. The angle between them changes and their lengths change as you move around the space. The instructions at the bottom of the frame say
Make A*x perpendicular to A*y
The SVD
When you reach the configuration where not only x is perpendicular to y but also Ax is perpendicular to Ay, you have found the singular value decomposition. The SVD is usually described as the matrix factorization
$$ A = U \Sigma V^T $$
with orthogonal $U$ and $V$ and diagonal $\Sigma$. This can be written
$$ A V = U \Sigma $$
For each column of $V$ and the corresponding column of $U$,
$$ A v_j = \sigma_j u_j $$
We can see that when Ax is perpendicular to Ay, the vectors x and y are the columns of $V$ and the vectors Ax and Ay are the columns of $U \Sigma$. The blue curve, which is the image of the unit circle under the transformation induced by $A$, is an ellipse. The vectors Ax and Ay are its major and minor axes and the half lengths of these axes are the singular values of the matrix.
For this first matrix it looks like the length of Ax might be about 1.25 and the length of Ay might be about 0.50. We can check this by actually computing the singular values.
format short
sigma = svd(A)
sigma =
1.2792
0.4886
Existence
In our previous posts about eigenvalues, we found that real eigenvectors don't always exist. If the eigenvectors are complex, eigshow can never find them. And if the matrix is defective, eigshow finds only one eigenvector, not the usual two. The situation is quite different for SVD. The real singular value decomposition always exists. It is always possible to rotate x and y to a position that makes Ax orthogonal to Ay.
In the language of abstract linear algebra, we say that the green vectors are an orthonormal basis for the domain of the transformation and, if the blue vectors were scaled to have unit length, they would be an orthonormal basis for the range of the transformation.
A defective matrix
Our final matrix in the eigenvalues post was defective -- it had only one eigenvector. But its SVD is obtained with no difficulty.
format rat
A = [6 4; -1 2]/4
A =
3/2 1
-1/4 1/2

At first it looks like the final blue vectors happen to be parallel to the display axes. This would say that the matrix $U$ in the SVD is the identity matrix. But a careful look at the final result shows slight stair-stepping in Ax and Ay. This is confirmed by actually computing the full SVD and observing that $U$ is not quite the identity.
format short
[U,S,V] = svd(A)
U =
-0.9991 -0.0424
-0.0424 0.9991
S =
1.8042 0
0 0.5542
V =
-0.8247 -0.5655
-0.5655 0.8247
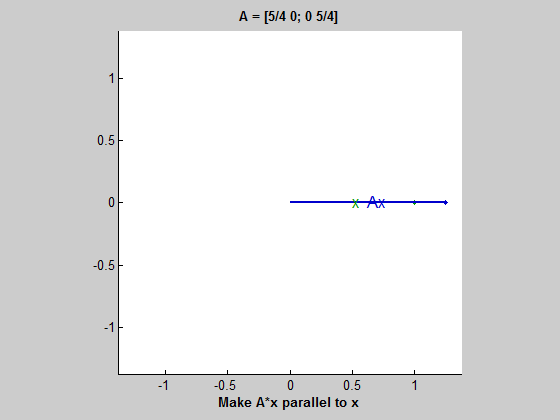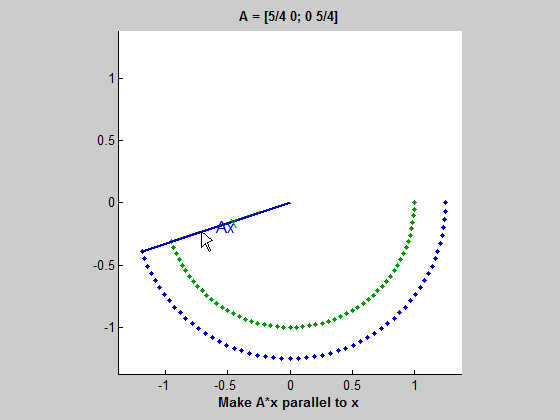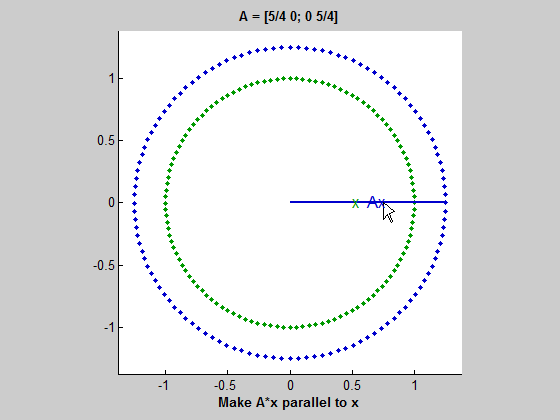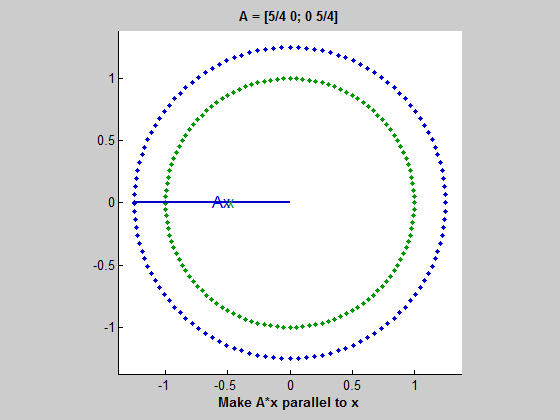
A singular matrix
Our singular example turns out to be a little tricky because the blue ellipse collapses to a one-dimensional line segment. It is hard to tell when Ax is perpendicular to Ay. It turns out to be when one of them is the zero vector; in other words, when x or y is the null vector of A. When one of Ax or Ay reaches zero, the other reaches its maximum length, the half-length of the line segment. This length is the nonzero singular value.
format rat
A = [2 4; 2 4]/4
A =
1/2 1
1/2 1

- Category:
- Eigenvalues,
- Matrices
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building






Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.