Anatomy of a Cube
A cube is the familiar three-dimensional solid with eight vertices, six faces and twelve edges. I have been working with cubes recently in posts about both the Menger sponge fractal and the 4-by-4 matrix from computer graphics.
Contents
Vertices
Cartesian coordinates, V, for the eight vertices of a cube can be generated from the binary representation of 0:7.
j = (0:7)'
j =
0
1
2
3
4
5
6
7
k = dec2bin(j)
k =
8×3 char array
'000'
'001'
'010'
'011'
'100'
'101'
'110'
'111'
V = double(k-'0')
V =
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
Edges
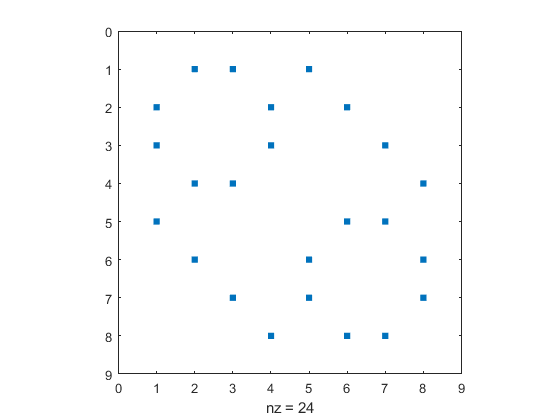
The twelve edges of a cube are described by the adjacency matrix A of connections between its vertices.
A = adjacency(V)
spy(A)
A =
0 1 1 0 1 0 0 0
1 0 0 1 0 1 0 0
1 0 0 1 0 0 1 0
0 1 1 0 0 0 0 1
1 0 0 0 0 1 1 0
0 1 0 0 1 0 0 1
0 0 1 0 1 0 0 1
0 0 0 1 0 1 1 0
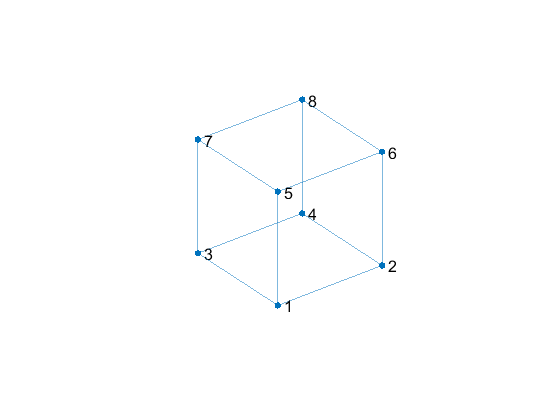
Wireframe
A plot of the graph of A provides a wireframe view of our cube.
G = graph(A);
p = plot(G, ...
NodeLabel = string(k), ...
NodeFontSize = 12, ...
XData = V(:,3), ...
YData = V(:,2), ...
ZData = V(:,1));
axis([-1 4 -1 4 -1 4]/3)
axis square off vis3d
view(3)

Let's replace the node labels with 1-based indices for rows of V.
p.NodeLabel = string(j+1);
Faces
A cube has six square faces. This array F provides the indices in V of the coordinates of the corners of each face. The ordering ensures that the normal to each face points out of the cube.
F = [ 1 5 7 3
3 7 8 4
1 3 4 2
2 4 8 6
1 2 6 5
5 6 8 7 ]
F =
1 5 7 3
3 7 8 4
1 3 4 2
2 4 8 6
1 2 6 5
5 6 8 7
If you Google "rgb gold", you will get links to Web sites offering red-green-blue values for dozens of shades of the color gold. My forthcoming post about the complement of the Menger sponge fractal uses just two shades.
gold = [212 175 55]/256
dark = gold/2
gold =
0.8281 0.6836 0.2148
dark =
0.4141 0.3418 0.1074
The single patch formed from V and F is just the skin enclosing our cube; its inside is hollow.
cla
patch(Faces = F, ...
Vertices = V, ...
FaceColor = gold, ...
EdgeColor = dark, ...
LineWidth = 1.5);
axis([-1 4 -1 4 -1 4]/3)
axis square off vis3d
view(3)

- Category:
- Graphics,
- Graphs,
- Programming



Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.