An Interesting, and Perhaps New, Matrix
I do not recall having seen this matrix before, but I will not be surprised to learn that somebody else already knows all about it, especially if that person's name is Nick.
Contents
Q
I've been investigating the matrices generated by this elegant one-liner.
Q = @(n) (-n:n).^2 + (-n:n)'.^2;
The Q is for "quadratic".
The middle column contains the squares of the integers from -n to n. So does the middle row. The apostrophe summons singleton expansion. The resulting matrix has order 2*n+1. Here is Q(5).
Q5 = Q(5)
Q5 =
50 41 34 29 26 25 26 29 34 41 50
41 32 25 20 17 16 17 20 25 32 41
34 25 18 13 10 9 10 13 18 25 34
29 20 13 8 5 4 5 8 13 20 29
26 17 10 5 2 1 2 5 10 17 26
25 16 9 4 1 0 1 4 9 16 25
26 17 10 5 2 1 2 5 10 17 26
29 20 13 8 5 4 5 8 13 20 29
34 25 18 13 10 9 10 13 18 25 34
41 32 25 20 17 16 17 20 25 32 41
50 41 34 29 26 25 26 29 34 41 50
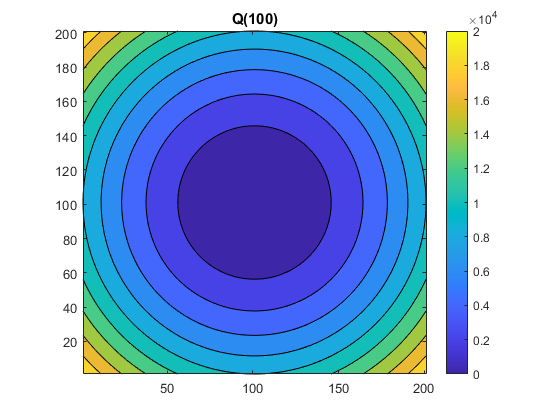
I like the contour plot.
contourf(Q(100))
axis square
colorbar
title('Q(100)')
D
For another blog post under development, I need a logical mask that carves a circular region out of graphic. This disc does the job.
D = @(n) Q(n) <= n^2;
Here is my carver.
spy(D(100))
title('D(100)')
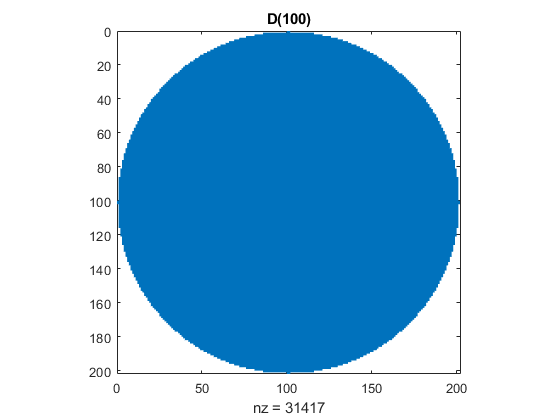
Did you notice the digits in the count of nonzeros in D(100)? It happens whenever n is a power of 10.
fprintf('%15s %12s\n','n','nnz(D(n))') for n = 10.^(0:4) fprintf('%15d %12d\n',n, nnz(D(n))) end
n nnz(D(n))
1 5
10 317
100 31417
1000 3141549
10000 314159053
O.E.I.S.
A classic problem, described in the Online Encyclopedia of Integer Sequences, asks how many points with integer coordinates lie within a disc of increasing radius. Our nonzero count provides the answer.
fprintf('%15s %8s\n','n','a(n)') for n = [1:15 99:101 499:501 999:1001] if mod(n,100) == 99 fprintf('%15s %8s\n','-','-') end a(n) = nnz(D(n)); fprintf('%15d %8d\n',n,a(n)) end
n a(n)
1 5
2 13
3 29
4 49
5 81
6 113
7 149
8 197
9 253
10 317
11 377
12 441
13 529
14 613
15 709
- -
99 30757
100 31417
101 32017
- -
499 782197
500 785349
501 788509
- -
999 3135157
1000 3141549
1001 3147833
R
Taking the reciprocals of the matrix entries, and reducing the range of the anonymous index, produces a matrix that behaves a bit like the Hilbert matrix, hilb(n).
R = @(n) 1./((1:n).^2 + (1:n)'.^2);
Here are the 5-by-5's.
format rat
R5 = R(5)
H5 = hilb(5)
R5 =
1/2 1/5 1/10 1/17 1/26
1/5 1/8 1/13 1/20 1/29
1/10 1/13 1/18 1/25 1/34
1/17 1/20 1/25 1/32 1/41
1/26 1/29 1/34 1/41 1/50
H5 =
1 1/2 1/3 1/4 1/5
1/2 1/3 1/4 1/5 1/6
1/3 1/4 1/5 1/6 1/7
1/4 1/5 1/6 1/7 1/8
1/5 1/6 1/7 1/8 1/9
Condition
Going away from the diagonal, the elements of R(n) decay more rapidly than those of hilb(n), so R(n) is better conditioned than hilb(n).
format short e fprintf('%15s %12s %12s\n','n','cond R','cond H') for n = 1:12 fprintf('%15d %12.2e %12.2e\n',n,cond(R(n)),cond(hilb(n))) end
n cond R cond H
1 1.00e+00 1.00e+00
2 1.53e+01 1.93e+01
3 2.04e+02 5.24e+02
4 2.59e+03 1.55e+04
5 3.21e+04 4.77e+05
6 3.89e+05 1.50e+07
7 4.67e+06 4.75e+08
8 5.54e+07 1.53e+10
9 6.53e+08 4.93e+11
10 7.65e+09 1.60e+13
11 8.92e+10 5.22e+14
12 1.04e+12 1.62e+16
Extra Credit
What is the rank of Q(n)? Why? See a paper in SIAM Review by Strang and Moler.
Why is the table of values for nnz(D(10^k)) so short? How might you extend this table?
Investigate R(n). Is it positive definite? What are its eigenvalues? What is its inverse? What is the sign pattern of the elements of its inverse? For what values of n can you compute the inverse reliably using floating point arithmetic? How does all this compare with hilb(n) and invhilb(n) ?
Comments in the Comments, or in email to me, are welcome.
- Category:
- Fun,
- History,
- Matrices,
- Numerical Analysis
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.