R2-D2, Rotations and Dilations in Two Dimensions
R2_D2 is is the name I've given a new MATLAB program that provides animations of 2-by-2 rotation and dilation matrices. I admit I chose "dilations" so the acronym would be memorable, but otherwise the code has little to do with the famous Star Wars droid.
Contents
House
This outline of a house is featured in Experiments with MATLAB. The data are the 11 blue dots. The coordinates of each dot form a 2-by-1 vector; the 2-by-2 rotation and dilation matrices multiply each of these vectors separately. (The lines between the dots complete the picture and are not involved in any computation.)
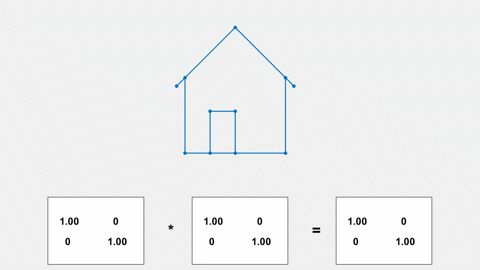
The house also appears in several editions of Gil Strang's textbooks. The cover of the third edition of Strang's Introduction to Linear Algebra features nine houses on a quilt made by Gil's friend Chris Curtis.

Hand
This outline of a hand, which I made from measurements of my own hand, is also used in Experiments with MATLAB. There are 37 points, so Hand is a 2-by-37 matrix.

Rotation
Multiplication by this matrix produces a two-dimensional rotation by an angle theta.
$$ R = \left( \begin{array}{rr} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{array} \right) $$
R is displayed in the first panel. If the house is not rotating in your browser, try this link: https://blogs.mathworks.com/cleve/files/house_rotate.gif

Dilation
Dilation is the process of making objects larger or smaller. Multiplication by this diagonal matrix produces a dilation by a factor sigma.
$$ S = \left( \begin{array}{rr} \sigma & 0 \\ 0 & \sigma \end{array} \right) $$
S is displayed in the second panel. The animation is also available at: https://blogs.mathworks.com/cleve/files/hand_dilate.gif

Both
Here rotation and dilation are combined. The product of the rotation and dilation matrices drives the action. If you are missing all the action, try: https://blogs.mathworks.com/cleve/files/hand_both.gif

R2_D2
When you run R2_D2 on your own computer, you can drive the rotations and dilations yourself. Mousing outside of the object creates rotation and mousing inside produces dilation.
The R2_D2 program is available from https://blogs.mathworks.com/cleve/files/R2_D2_14.m
Further Reading
If you are not familiar with matrices, or just want a quick refresher, check out the Matrices chapter of Experiments with MATLAB. Exercise 4.14 is particularly handy.
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building







Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.