
The Bucky Ball provides an elegant example of a graph, the connectivity of the Buckminster Fuller geodesic dome.We are also demonstrating publishing this blog with the Live Editor. There is a button... 더 읽어보기 >>

The Bucky Ball provides an elegant example of a graph, the connectivity of the Buckminster Fuller geodesic dome.We are also demonstrating publishing this blog with the Live Editor. There is a button... 더 읽어보기 >>
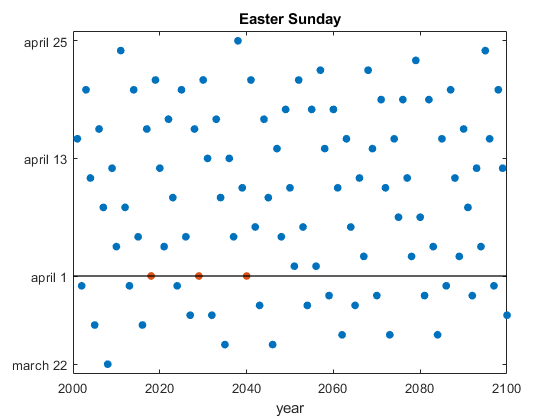
What do the years 2018, 2029 and 2040 have in common? They are the only years in the 21st century when Easter Sunday occurs on April Fools Day.... 더 읽어보기 >>

A news story released yesterday, March 31,by c|net has the headline... 더 읽어보기 >>

What do Mount St. Helens and the rank of a matrix have in common? The answer is the MATLAB function peaks. Let me explain. Please bear with me -- it's a long story.... 더 읽어보기 >>

Alexa tells me that the definition of serendipity is "the occurrence and development of events by chance in a happy or beneficial way."... 더 읽어보기 >>

A Mesmerizing AnimationWe are working on a paper about the Kuramoto model of self-synchronizing oscillators. This animation shows the different initial conditions where six oscillators fail to... 더 읽어보기 >>
It has been a while since I made a blog post. It is because I am preparing to give a talk next week on"The Evolution of the Evolution of MATLAB"on E-NLA, the Online seminar series on Numerical... 더 읽어보기 >>

(A slight revision of the post I made a few hours ago.)... 더 읽어보기 >>

Lots of tiny bubbles.... 더 읽어보기 >>
