Points and Polygons

Contents

Polygons

Polygons in two dimensions are generally represented in MATLAB with two arrays, locations for the X vertices and Y vertices. There is no need to have the final points in these match the initial points; that is, when arrays as described are used in situations where they are interpreted as polygon vertices, the polygon is automatically closed.

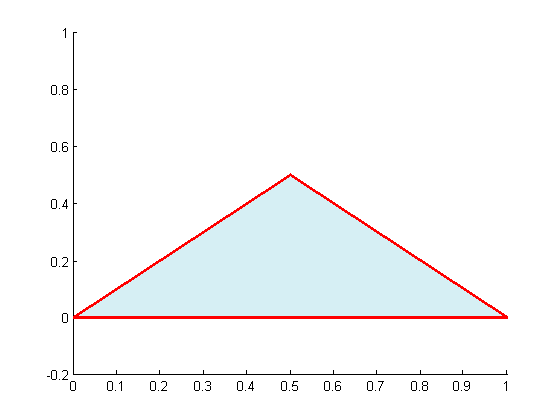
Let's define a very simple polygon to start.

X = [0 0.5 1]';
Y = [0 0.5 0]';

And look at it.

patch(X,Y, [0.2, 0.7, 0.8], 'edgecolor','r',...
    'facealpha', 0.2, 'linewidth',2);
axis([0 1 -0.2 1])

Some Points of Interest

Let's create some points of interest now. Some inside, some outside, and some on the boundary.

xin = [0.3 0.75 0.82]';
yin = [0.25 0.1, 0.05]';
xout = [0.3 0.75 0.82]';
yout = [-0.15 0.6, 0.3]';
xedge = [0.3 0.75 0.82]';
yedge = [0.3 0.25, 0.18]';
hold all
plot(xin, yin, 'g*', 'markersize',5)
plot(xout, yout, 'mx', 'markersize',9)
plot(xedge, yedge, 'bd', 'markersize',7)
hold off

Test the Points with the Polygon

[inIN onIN] = inpolygon(xin,yin, X, Y)

inIN =
     1
     1
     1
onIN =
     0
     0
     0

[inOUT onOUT] = inpolygon(xout,yout, X, Y)

inOUT =
     0
     0
     0
onOUT =
     0
     0
     0

[inEDGE onEDGE] = inpolygon(xedge,yedge, X, Y)

inEDGE =
     1
     1
     1
onEDGE =
     1
     1
     1

Multiply-connected Polygon

Here's an example from the help for inpolygon, with a square containing a square hole. The outer loop is counterclockwise, the inner clockwise.

xv = [0 3 3 0 0 NaN 1 1 2 2 1];
yv = [0 0 3 3 0 NaN 1 2 2 1 1];
x = rand(1000,1)*3; y = rand(1000,1)*3;
in = inpolygon(x,y,xv,yv);
plot(xv,yv,x(in),y(in),'.r',x(~in),y(~in),'.b')

Do You Work with Points and Polygons?

Have you used inpolygon? I'd love to hear the contexts of the problems you solve with it.

Get the MATLAB code

Published with MATLAB® 7.11