Thoughts about Anonymous Functions
One of the reasons I like using anonymous functions is because they allow me to express whatever function I want to use as a function of the relevant arguments in different contexts.
Contents
Example
Here's a very general way I can write the code meant to generate points on a straight line.
straightline = @(X,slope,intercept) slope*X + intercept
straightline =
@(X,slope,intercept)slope*X+intercept
Choose a Particular Line to Plot
First let's choose a particular straight line segment. I start by defining the slope and intercept values.
m = 2; % slope b = -3; % intercept
Plot the Line
Now I can evaluate my function when I create the plot.
x = 2:0.1:5; plot(x,straightline(x,m,b))
Find Area Under the Line
Now let's find the area under a segment of this line, between two points. Since the function integral requires the integrand to be a function of one variable only, we can use the anonymous function myline, defined below, to create just such a representation.
lowerlimit = 2; upperlimit = 5;
Create a function representing my particular line segment, by fixing those slope and intercept values, and creating a new function from the original one.
myline = @(x) straightline(x,m,b);
Use this new function, myline, as the integrand.
myarea = integral(myline, lowerlimit, upperlimit)
myarea =
12
Find Best Fit Line
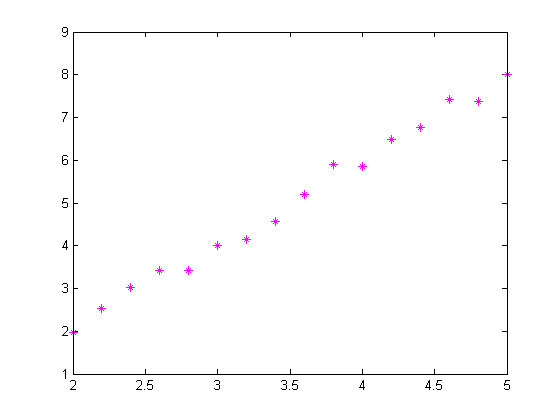
Now suppose we have data, based on this line segment, that has some noise. And we would like to estimate the slope and intercept values.
m = 2;
b = -2;
t = (2:0.2:5)';
data = straightline(t,m,b) + 0.2*randn(size(t));
plot(t,data,'m*')
Now I want slope and intercept to be my independent variables. I can use polyfit. Of course, I could use \ as well.
p = polyfit(t,data,1);
Now compare estimates for slope and intercept to original values.
comparison = [m, b; p]
comparison =
2 -2
2.094 -2.3638
Perhaps I instead want a function of the slope and intercept only. In that case, with data supplied, I can derive such a function from straightline. I can even get the values put into a
slopeIntercept = @(slope,intercept) straightline(data, slope, intercept); slp = [1 4]; intcpt = [0 -5]; newline1 = @(X) straightline(X, slp(1), intcpt(1)); newline2 = @(X) straightline(X, slp(2), intcpt(2));
Anonymous Functions Allow Interface Flexibility
Using the same original function definition for straightline, I am able to mold the function for different purposes. In the first case, I turned my function of 3 variables into a function of one variable, with preset parameters. I could also use it to create a function of just slope and intercept, suitable for create line segments for different parameters at a later time.
In fact, if I was trying to use my straightline function with some other code that required lines to be defined by slope and intercept first, and then the abscissa, I can easily create a new interface for the line.
differentLine = @(slope, intercept, X) straightline(X, slope, intercept);
Have You Used Anonymous Functions to Alter the Interface?
I'd love to hear your thoughts here.









댓글
댓글을 남기려면 링크 를 클릭하여 MathWorks 계정에 로그인하거나 계정을 새로 만드십시오.