Thoughts about Anonymous Functions
One of the reasons I like using anonymous functions is because they allow me to express whatever function I want to use as a function of the relevant arguments in different contexts.
Contents
Example
Here's a very general way I can write the code meant to generate points on a straight line.
straightline = @(X,slope,intercept) slope*X + intercept
straightline =
@(X,slope,intercept)slope*X+intercept
Choose a Particular Line to Plot
First let's choose a particular straight line segment. I start by defining the slope and intercept values.
m = 2; % slope b = -3; % intercept
Plot the Line
Now I can evaluate my function when I create the plot.
x = 2:0.1:5; plot(x,straightline(x,m,b))
Find Area Under the Line
Now let's find the area under a segment of this line, between two points. Since the function integral requires the integrand to be a function of one variable only, we can use the anonymous function myline, defined below, to create just such a representation.
lowerlimit = 2; upperlimit = 5;
Create a function representing my particular line segment, by fixing those slope and intercept values, and creating a new function from the original one.
myline = @(x) straightline(x,m,b);
Use this new function, myline, as the integrand.
myarea = integral(myline, lowerlimit, upperlimit)
myarea =
12
Find Best Fit Line
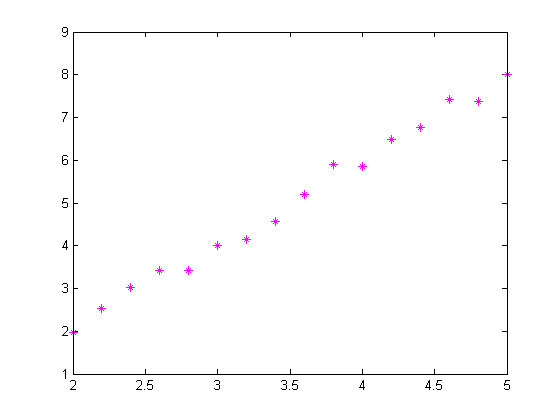
Now suppose we have data, based on this line segment, that has some noise. And we would like to estimate the slope and intercept values.
m = 2;
b = -2;
t = (2:0.2:5)';
data = straightline(t,m,b) + 0.2*randn(size(t));
plot(t,data,'m*')
Now I want slope and intercept to be my independent variables. I can use polyfit. Of course, I could use \ as well.
p = polyfit(t,data,1);
Now compare estimates for slope and intercept to original values.
comparison = [m, b; p]
comparison =
2 -2
2.094 -2.3638
Perhaps I instead want a function of the slope and intercept only. In that case, with data supplied, I can derive such a function from straightline. I can even get the values put into a
slopeIntercept = @(slope,intercept) straightline(data, slope, intercept); slp = [1 4]; intcpt = [0 -5]; newline1 = @(X) straightline(X, slp(1), intcpt(1)); newline2 = @(X) straightline(X, slp(2), intcpt(2));
Anonymous Functions Allow Interface Flexibility
Using the same original function definition for straightline, I am able to mold the function for different purposes. In the first case, I turned my function of 3 variables into a function of one variable, with preset parameters. I could also use it to create a function of just slope and intercept, suitable for create line segments for different parameters at a later time.
In fact, if I was trying to use my straightline function with some other code that required lines to be defined by slope and intercept first, and then the abscissa, I can easily create a new interface for the line.
differentLine = @(slope, intercept, X) straightline(X, slope, intercept);
Have You Used Anonymous Functions to Alter the Interface?
I'd love to hear your thoughts here.
- Category:
- Function Handles,
- How To
 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Guy on Simulink
Guy on Simulink MATLAB Community
MATLAB Community Artificial Intelligence
Artificial Intelligence Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs Autonomous Systems
Autonomous Systems Quantitative Finance
Quantitative Finance MATLAB Graphics and App Building
MATLAB Graphics and App Building








Comments
To leave a comment, please click here to sign in to your MathWorks Account or create a new one.